home 1 2 3 4 5 6 7 8 9 10 11 12 13 Print

Section 11.1: Inference about Two Proportions

Objectives

By the end of this lesson, you will be able to...

  1. test hypotheses regarding two population proportions
  2. construct and interpret confidence intervals for the difference between two population proportions
  3. determine the sample size necessary for estimating the difference between two population proportions within a specific margin of error

For a quick overview of this section, watch this short video summary:

In Chapters 9 and 10, we studied inferential statistics (confidence intervals and hypothesis tests) regarding population parameters of a single population - the average rest heart rate of students in a class, the proportion of ECC who voted, etc.

In Chapter 11, we'll be considering the relationship between two populations - means, proportions and standard deviaions.

A frequent comparison we want to make between to populations is concerning the proportion of individuals with certain characteristics. For example, suppose we want to determine if college faculty voted at a higher rate than ECC students in the 2008 presidential election. Since we don't have any information from either population, we would need to take samples from each. This isn't an example of a hypothesis test from Section 10.4, about one proportion, it'd be comparing two proportions, so we need some new background.

The information that follows is a bit heavy, but it shows the theoretical background for testing claims and finding confidence intervals for the difference between two population proportions.

The Difference Between Two Population Proportions

In Section 8.2, we discussed the distribution of one sample proportion, p-hat. What we'll need to do now is develop some similar theory regarding the distribution of the difference in two sample proportions, p1-p2.

The Sampling Distribution of the Difference between Two Proportions

Suppose simple random samples size n1 and n2 are taken from two populations. The distribution of p1-p2 where p1 and p2, is aproximately normal with mean mean of p1-p2 and standard deviation
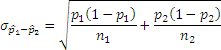standard deviation of p1-p2, provided:

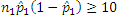
  1. condition 1
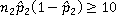
  2. condition 2
  3. both sample sizes are less than 5% of their respective populations.

The standardized version is then

z

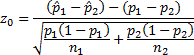
which has an approximate standard normal distribution.

 

The thing is, in most of our hypothesis testing, the null hypothesis assumes that the proportions are the same (p1 = p2), so we can call p = p1 = p2.

Since p1 = p2, we can substitute 0 for p1–p2, and substitute p for both p1 and p2. In that case, we can rewrite the above standardized z the following way:

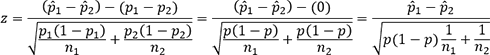
z formula

Which leads us to our hypothesis test for the difference between two proportions.

Performing a Hypothesis Test Regarding p1–p2

Step 1: State the null and alternative hypotheses.

Two-Tailed
H0: p1–p2 = 0
H1: p1–p2 ≠ 0		 Left-Tailed
H0: p1–p2 = 0
H1: p1–p2 < 0		 Right-Tailed
H0: p1–p2 = 0
H1: p1–p2 > 0

Step 2: Decide on a level of significance, α.

Step 3: Compute the test statistic, 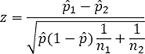test statistic.

Step 4: Determine the P-value.

Step 5: Reject the null hypothesis if the P-value is less than the level of significance, α.

Step 6: State the conclusion.

A note about the difference between two proportions: As with the previous two sections, the order in which the proportions are placed is not important. The important thing is to note clearly in your work what the order is, and then to construct your alternative hypothesis accordingly.

Hypothesis Testing Regarding p1–p2 Using StatCrunch

With Data

  1. Select Stat > Proportion Stats > Two Sample > With Data
  2. Select the variable names. If the values are in a single column, select the column and use the Where box to identify the two samples.
  3. Type the Successes exactly as they appear in the data, including capitalization and spacing.
  4. Set the null and alternative hypotheses.
  5. Click Compute.

With Summary

  1. Select Stat > Proportion Stats > Two Sample > With Summary
  2. Enter the number of successes* and the number of observations*.
  3. Set the null and alternative hypotheses.
  4. Click Compute.

* To get the counts, first create a frequency table. If you have a grouping variable, use a contingency table.

Example 1

Problem: Suppose a researcher believes that college faculty vote at a higher rate than college students.  She collects data from 200 college faculty and 200 college students using simple random sampling.  If 167 of the faculty and 138 of the students voted in the 2008 Presidential election, is there enough evidence at the 5% level of significance to support the researcher’s claim?

Solution:

First, we need to check the conditions. Both sample sizes are clearly less than 5% of their respective populations. In addition,

conditions

So our conditions are satisfied.

Step 1:

Let's take the two portions in the order we receive them, so
p1 = pf (faculty) and p1= ps (students)

Our hypotheses are then:
H0: pf - ps = 0
H1: pf - ps > 0 (since the researcher claims that faculty vote at a higher rate)

Step 2: α = 0.05 (given)

Step 3: (we'll use StatCrunch)

Step 4: Using StatCrunch:

StatCrunch calculation
(Trimmed to fit on this page.)

Step 5: Since the P-value < α, we reject the null hypothesis.

Step 6: Based on these results, there is very strong evidence (certainly enough at the 5% level of significance) to support the researcher's claim.

Confidence Intervals about the Difference Between Two Proportions

We can also find a confidence interval for the difference in two population proportions.

In general, a (1-α)100% confidence interval for p1-p2is

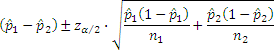
CI formula

Note: The following conditions must be true:

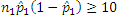
  1. condition 1
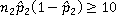
  2. condition 2
  3. both sample sizes are less than 5% of their respective populations.

Confidence Intervals About p1-p2 Using StatCrunch

With Data

  1. Select Stat > Proportion Stats > Two Sample > With Data
  2. Select the variable names. If the values are in a single column, select the column and use the Where box to identify the two samples.
  3. Type the Successes exactly as they appear in the data, including capitalization and spacing.
  4. Check the confidence interval radio button.
  5. Set the confidence level.
  6. Click Compute.

With Summary

  1. Select Stat > Proportion Stats > Two Sample > With Summary
  2. Enter the number of successes* and the number of observations*.
  3. Check the confidence interval radio button.
  4. Set the confidence level.
  5. Click Compute.

* To get the counts, first create a frequency table. If you have a grouping variable, use a contingency table.

Example 2

Problem: Considering the data from Example 1, find a 99% confidence interval for the difference between the proportion of faculty and the proportion of students who voted in the 2008 Presidential election.

Solution: From Example 1, we know that the conditions for performing inference are met, so we'll use StatCrunch to find the confidence interval.

StatCrunch calculation
(Timmed to fit on this page.)

So we can say that we're 99% confident that the difference between the proportion of faculty who vote and the proportion of students who vote is between 3.7% and 25.3%.

Determining the Sample Size Needed

In Section 9.3, we learned how to find the necessary sample size if a specific margin of error is desired. We can do a similar analysis for the difference in two proportions. From the confidence interval formula, we know that the margin of error is:

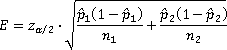
margin of error

If we assume that n1 = n2 = n, we can solve for n and get the following result:

The sample size required to obtain a (1-α)100% confidence interval for p1-p2with a margin of error E is:

sample size needed

rounded up to the next integer, if p1-hat and p2-hat are esimates for p1 and p2, respectively.

If no prior estimate is available, use no prior estimate, which yields the following formula:

sample size needed

again rounded up to the next integer.

Note: As in Section 9.3, the desired margin of error should be expressed as a decimal.

Let's try one.

Example 3

Suppose we want to study the success rates for students in Mth098 Intermediate Algebra at ECC.  We want to compare the success rates of students who place directly into Mth098 with those who first took Mth096 Beginning Algebra.  From past experience, we know that a typical success rate for students in this class is about 65%.  How large of a sample size is necessary to create a 95% confidence interval for the difference of the two passing rates with a maximum error of 2%?

[ reveal answer ]

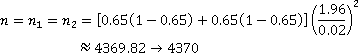
calculation

So we would need a sample size of 4,370 students - from each population!

 

 

<< previous section | next section >>

home 1 2 3 4 5 6 7 8 9 10 11 12 13 Print