Section 11.3: Inference about Two Standard Deviations

Objectives

By the end of this lesson, you will be able to...

find critical values of the F-distribution
test hypotheses regarding two population standard deviations

For a quick overview of this section, watch this short video summary:

The last parameters we need to compare between two populations are the variance and standard deviation. Before we can develop a hypothesis test comparing two population parameters, we need another distribution.

Fisher's F-distribution

Unlike the mean, the standard deviation is extremely susceptible to extreme values, and consequently does a very poor job of measuring spread for distributions that are not symmetric. So before we do any inference regarding population standard deviations, we must first verify that the samples come from normally distributed populations.

Fisher's F-distribution

If and and are sample variances from independent simple random samples of size n₁and n₂, respectively, drawn from normal populations, then

follows the F-distribution with n₁-1 degrees of freedom in the numerator and
n₂-1 degrees of freedom in the denominator.

Properties of the F-distribution

Like the Χ² distribution, it is not symmetric. It is skewed right
The shape depends on the degrees of freedom in the numerator and denominator.
F≥0

Notice here that the samples must come from normally distributed populations.

Finding Critical Values

Find critical values in the F-distribution using a table is done in a similar manner to the t and Χ² tables, though with some differences. The values in the table still represent values with the indicidated α area to the right, but because the F distribution has two degreees of freedom rather than one, it requires a separate table for each α.

Before we start the section, you need a copy of the table. You can download a printable copy of this table, or use a copy from a textbook. That table will look different than the printable version linked above because the publisher did not provide a digital version.

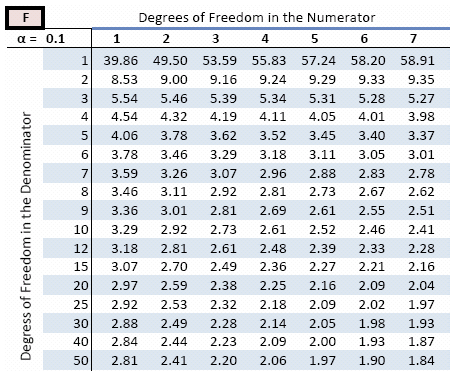
t-table

So the values in the table above are the critical values:

You may wonder how we find critical values for left-tailed tests. To do that, we use the same table and the following formula:

Let's try a couple examples.

Example 1

Find the value of the F-distribution that has α=0.05 area to the right, with 10 degrees of freedom in the numerator, and 15 degrees of freedom in the denominator.

[ reveal answer ]

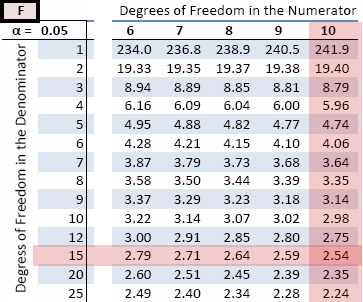
f-table

So F_{0.05, 10, 15} = 2.54

Example 2

Find the value of the F-distribution that has α=0.05 area to the left, with 20 degrees of freedom in the numerator, and 8 degrees of freedom in the denominator.

[ reveal answer ]

F_{0.95, 20, 8} =	1		1	≈ 0.41
	F_{0.05, 8, 20}		2.45

Finding Critical Values Using StatCrunch

Click on Stat > Calculators > F

Enter the numerator and denominator degrees of freedom, the direction of the inequality, and the probability (leave X blank). Then press Compute.

Example 3

Use the technology of your choice to find the value from the F-distribution with α=0.01 area to the right if samples of size 15 and 20 are taken.

[ reveal answer ]

Using StatCrunch:

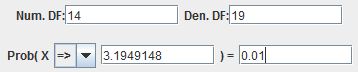
StatCrunch calculation

So F_{0.01, 14, 19} = 3.19

Performing a Hypothesis Test Regarding Two Population Standard Deviations

Step 1: State the null and alternative hypotheses.

Two-Tailed
H₀:

H₁:

Left-Tailed
H₀:

H₁:

Right-Tailed
H₀:

H₁:

Step 2: Decide on a level of significance, α.

Step 3: Compute the test statistic, .

Step 4: Determine the P-value.

Step 5: Reject the null hypothesis if the P-value is less than the level of significance, α.

Step 6: State the conclusion.

Hypothesis Testing Regarding Two Population Standard Deviations Using StatCrunch

Go to Stat > Variance > Two Sample > With Data/Summary
If using data, select the appropriate columns for the two samples. If the values are in a single column, select the column and use the Where box to identify the two samples. If you are using a summary, enter the sample variances* and sample sizes.
Set the null variance ratio (standard is 1) and the alternative hypothesis.
Click on Calculate.

The results should appear.

Example 4

Problem:In Example 1 in Section 11.2, we compared the average scores of men and women on a Mth096 exam. In that test, we assumed that the standard deviations of the two groups were equal. Test the assumption at the α=0.1 level of significance.

Solution:

First, we need to check the conditions. We know from Example 1 that neither sample contains outliers, but we do not know if they come from normally distributed populations. We'll use StatCrunch to perform Q-Q plots.

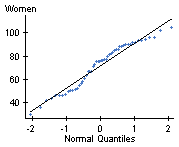
While the two plots aren't exactly linear, it does appear that the samples could come from normally distributed populations, so our conditions are satisfied.

Step 1:
H₀:
H₁:

Step 2: α = 0.1 (given)

Step 3: (we'll use StatCrunch)

Step 4: Using StatCrunch:

StatCrunch calculation

Step 5: Since the P-value > α, we do not reject the null hypothesis.

Step 6: Based on these results, there is no evidence to support the claim that the standard deviations are not equal.