home 1 2 3 4 5 6 7 8 9 10 11 12 13 Print

Section 10.4: Hypothesis Tests for a Population Standard Deviation

Objectives

By the end of this lesson, you will be able to...

  1. test hypotheses about a population standard deviation

For a quick overview of this section, watch this short video summary:

Before we begin this section, we need a quick refresher of the Χ2 distribution.

The Chi-Square (Χ2) distribution

Reminder: "chi-square" is pronounced "kai" as in sky, not "chai" like the tea.

The Chi-Square (Χ2) distribution

If a random sample size n is obtained from a normally distributed population with mean μ and standard deviation σ, then

chi-square

has a chi-square distribution with n-1 degrees of freedom.

chi-square distribution

Properties of the Χ2 distribution

  1. It is not symmetric.
  2. The shape depends on the degrees of freedom.
  3. As the number of degrees of freedom increases, the distribution becomes more symmetric.
  4. Χ2≥0

Finding Probabilities Using StatCrunch

Click on Stat > Calculators >Chi-Square

Enter the degrees of freedom, the direction of the inequality, and X. Then press Compute.

We again have some conditions that need to be true in order to perform the test 

  1. the sample was randomly selected, and
  2. the population from which the sample is drawn is normally distributed

Note that in the second requirement, the population must be normally distributed. The steps in performing the hypothesis test should be familiar by now.

Performing a Hypothesis Test Regarding σ

Step 1: State the null and alternative hypotheses.

Two-Tailed
H0: σ = σ0
H1: σ ≠ σ0		 Left-Tailed
H0: σ = σ0
H1: σ < σ0		 Right-Tailed
H0: σ = σ0
H1: σ > σ0

Step 2: Decide on a level of significance, α.

Step 3: Compute the test statistic, test statistic.

Step 4: Determine the P-value.

Step 5: Reject the null hypothesis if the P-value is less than the level of significance, α.

Step 6: State the conclusion.

Example 1

In Example 2, in Section 10.2, we assumed that the standard deviation for the resting heart rates of ECC students was 12 bpm. Later, in Example 2 in Section 10.3, we considered the actual sample data below.

heart rate
61 63 64 65 65
67 71 72 73 74
75 77 79 80 81
82 83 83 84 85
86 86 89 95 95

(Click here to open the data in StatCrunch.)

Based on this sample, is there enough evidence to say that the standard deviation of the resting heart rates for students in this class is different from 12 bpm?

Note: Be sure to check that the conditions for performing the hypothesis test are met.

[ reveal answer ]

From the earlier examples, we know that the resting heart rates could come from a normally distributed population and there are no outliers.

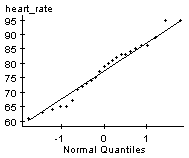
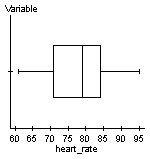
normal probability plot     boxplot

Step 1:
H0: σ = 12
H1: σ ≠ 12

Step 2: α = 0.05

Step 3: test statistic

Step 4: P-value = 2P(Χ2 > 15.89) ≈ 0.2159

Step 5: Since P-value > α, we do not reject H0.

Step 6: There is not enough evidence at the 5% level of significance to support the claim that the standard deviation of the resting heart rates for students in this class is different from 12 bpm.

Hypothesis Testing Regarding σ Using StatCrunch

  1. Select Stat > Variance > One Sample
  2. Select With Data if you have the data, or With Summary if you only have the summary statistics.
  3. If you chose With Data, click on the variable that you want for the hypothesis test. Otherwise, enter the sample statistics.
  4. Enter the population variance (not standard deviation!) and HA, then click Compute.

Example 2

Let's look at Example 1 again, and try the hypothesis test with technology.

[ reveal answer ]

Using StatCrunch:

StatCrunch calculation

 

<< previous section | next section >>

home 1 2 3 4 5 6 7 8 9 10 11 12 13 Print