Section 11.4: Putting It Together: Which Method Do I Use?
Objectives
By the end of this lesson, you will be able to...
- determine the appropriate hypothesis test to perform
Hypothesis Tests Regarding Two Populations
So we now have four new hypothesis tests to add to our arsenal. Here they are again:
Tests Regarding the Mean Difference
In order to perform a hypothesis test regarding two population means, the following must be true concerning a sample:
- the sample is obtained using simple random sampling, and
- the sample data are matched pairs, and
- the sample has no outliers and the population from which the sample is drawn is normally distributed, or the sample size is large (n≥30).
Then the test statistic is
![]()
Tests Regarding the Difference Between Two Population Means
In order to perform a hypothesis test regarding the mean difference, the following must be true:
- a simple random sample of size n1 is taken from a population with unknown mean μ1 and unknown standard deviation σ1
- a simple random sample of size n2 is taken from a second population with unknown mean μ2 and unknown standard deviation σ2
- the two populations are normally distributed or the sample sizes are sufficiently large (n1, n2≥30)
Then the test statistic is:
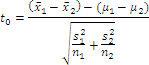
Tests Regarding the Difference Between Two Population Proportions
In order to perform a hypothesis test regarding the mean difference, the following must be true:
- simple random samples size n1 and n2 are taken from two populations
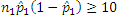
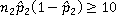
- both sample sizes are less than 5% of their respective populations.
Then the test statistic is:
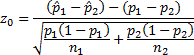
Tests Regarding Two Population Standard Deviations
In order to perform a hypothesis test regarding the mean difference, the following must be true:

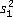 and
and 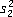 are
sample variances from independent simple random samples of size n1and
n2, respectively
are
sample variances from independent simple random samples of size n1and
n2, respectively- both populations are normal
Then the test statistic is:
![]()
Choosing the Appropriate Hypothesis Test
Now that we've done a (very) quick review of the four various tests, it's helpful to think of a flowchart when deciding which test to apply. Here's a version of the flowchart from your text:
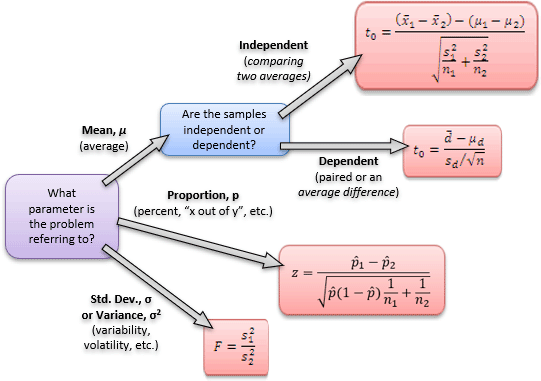
The biggest problems usually occur between the independent and dependent samples regarding the means. They key is to determine if the samples are somehow paired. A dead giveaway is a problem with before and after. In that case, they're clearly paired, making them dependent samples. If you're comparing two completely different populations (the average mpg for Honda Civics vs. Toyota Camry), then you have independent samples.
As we mentioned in the last chapter, there's no quick and easy rule to memorize. You'll need to practice all the problems on the following page and be sure to do all the assigned homework problems. There's also an extra review for this exam, which also helps you choose which hypothesis test to apply. It's important to practice, practice, practice!
Some Examples
It's time for examples. In each case, don't worry about actually completing the problem. Focus instead on choosing the correct hypothesis test to apply. For more practice, you should look at the Exam 4 Extra Review file, which is available in Desire2Learn.
Example 1
Janis commutes to her Statistics class at ECC. She has two possible routes and would like to determine which is optimal. To help decide, she collects travel times for 60 morning trips, 30 on each route. Her first route has an average travel time of 24.3 minutes, with a standard deviation of 3.8 minutes. The second route has an average travel time of 22.9 minutes, with a standard deviation of 4.4 minutes. Based on these data, does Janis have enough evidence to say that the second route is the optimal one?
Janis wants to compare the average commute time, so this is the comparison of two means. The various trips are not paired at all (she simply has 30 samples from each trip), so they are independent samples. The statistic we would use is:
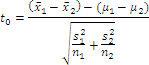
In this case, the null and alternative hypotheses would be:
| H0: μ1 - μ2 =
0 H1: μ1 - μ2 > 0 |
or | H0: μ1 = μ2 H1: μ1 > μ2 |
Example 2
Jay and Sheila are pig farmers in south-western Minnesota. They're changing the feed they use, and they're concerned that one of the new options leads to weights in the pigs that vary too widely. To help determine which choice of feed is more consistent, they take two samples of 100 piglets each. The first sample receives feed from AgraChoice, while the second receives feed from Swine Food. After 6 months, both samples have similar average weights of nearly 200 pounds, but the standard deviations are different. The AgraChoice sample has a standard deviation of 22.1 pounds, while the Swine Food sample has a standard deviation of 24.3 pounds.
Based on these samples, are Jay and Sheila's fears founded? Does the Swine Food yield 6-month-old pigs whose weight varies more than those fed with AgraChoice?
The key here is the use of the word vary. Any test concerning "variability" is regarding the standard deviation or variance. The test statistic for this problem would be the F-statistic:
![]()
And the null and alternative hypotheses would be:
If we choose population 1 to be those using the AgraChoice feed:
H0: ![]()
H1: ![]()
or
Choosing population 1 to be those using Swine Food:
H0: ![]()
H1: ![]()
In both cases, the direction for H1 is chosen because Jay and Sheila want to determine if the Swine Food feed yields pigs with more variability than those on the AgraChoice feed.
Example 3
A statistics professor is interested in the success rates of his students. In particular, anecdotal evidence seems to suggest that those students who are returning to college after an absence seem to be more successful in his courses. He collects data from his and his colleagues' students over one semester, specifically focusing on whether or not students were "returning" (defined for his purposes as those with two or more years away from school) and whether or not they were "successful" (earning a C or better).
He found that out of 184 "returning" students, 132 were successful, and of 429 "traditional" students, 256 were successful. Based on these data, is there evidence to support the professor's anecdotal evidence?
The key phrase here is "out of", which implies a proportion. This is then a comparison of two population proportions, with the test statistic
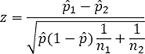
And null and alternative hypotheses of:
| H0: pR - pT = 0 H1: pR - pT > 0 |
or | H0: pR = pT H1: pR > pT |
(Using pR for the proportion of "returning" students and pT for the proportion of "traditional" students.)
Example 4
A college adminstrator recently learned about a new strategy for encouraging faculty participation in academic committees. She is prepared to implement it, and would like to know if it truly changes faculty participation. She chooses a random sample of 10 faculty and records their current attendance at committee meetings. She then implements the new strategy she learned and records the attendance of these same faculty. The data she collected are as follows (in meetings attended per month):
| Faculty: | A | B | C | D | E | F | G | H | I | J |
| Before | 1 | 2 | 2 | 4 | 3 | 2 | 2 | 3 | 3 | 0 |
| After | 2 | 2 | 2 | 2 | 3 | 1 | 1 | 1 | 2 | 2 |
Is there evidence to say the new strategy increased faculty participation in their committees?
The key here is that these are paired - before and after. In that case, the test statistic is:
![]()
And null and alternative hypotheses of:
H0: μd = 0
H1: μd < 0 *
* Note the order here is important. If we define d = before - after, and the question is whether the new strategy increased participation, we think the mean difference would be negative.
