Section 9.3: Confidence Intervals for a Population Standard Deviation
Objectives
By the end of this lesson, you will be able to...
- find critical values for the Χ2 distribution
- construct and interpret CIs about σ2 and σ
For a quick overview of this section, watch this short video summary:
The last parameters we need to find confidence intervals for are the population variance (σ2) and standard deviation (σ).
There are many instances where we might be interested in knowing something about the spread of a population based on a sample. For example, we might believe that a particular group of students seems to have a wider variation in their grades than those from the past. Or a part manufacturer may be concerned that one of the parts it's manufacturing is too inconsistent, even though the mean may be at specifications.
Before we can develop a confidence interval for the variance, we need another distribution.
The Chi-Square (Χ2) distribution
Note: "chi-square" is pronounced "kai" as in sky, not "chai" like the tea.
The Chi-Square (Χ2) distribution
If a simple random sample size n is obtained from a normally distributed population with mean μ and standard deviation σ, then
![]()
has a chi-square distribution with n-1 degrees of freedom.

Properties of the Χ2 distribution
- It is not symmetric.
- The shape depends on the degrees of freedom.
- As the number of degrees of freedom increases, the distribution becomes more symmetric.
- Χ2≥0
Finding Critical Values
Find critical values in the Χ2 distribution using a table is done in the same manner we found critical values for the t-distribution.
Before we start the section, you need a copy of the table. You can download a printable copy of this table, or use the table in the back of a textbook. It should look something like the image below (trimmed to make it more viewable).

Notice that the table is similar to the t-table, with probabilities along the top and critical values in the middle. This is because we primarily use the chi-square-table to find critical values.
Let's try an example.
Example 1
Find the critical values in the Χ2 distribution which separate the middle 95% from the 2.5% in each tail, assuming there are 12 degrees of freedom.
You can use the table above, or print one out yourself. Any textbook should also come with a copy you can use.

We can see form the table that the two critical values are 4.404 and 23.337.
Finding Critical Values Using StatCrunch
|
Click on Stat > Calculators > Chi-Square Enter the degrees of freedom, the direction of the inequality, and the probability (leave X blank). Then press Compute. |
Example 2
Use the technology of your choice to find Χ20.01 with 20 degrees of freedom.
Χ20.01,20 ≈ 37.566
Constructing Confidence Intervals about σ2 and σ
Now that we have the basics of the distribution of the variable Χ2, we can work on constructing a formula for the confidence interval.
From the distribution shape on the previous page, we know that ![]() of the Χ2 values will be between the two critical values shown below.
of the Χ2 values will be between the two critical values shown below.

This gives us the following inequality:
![]()
If we solve the inequality for σ2, we get the formula for the confidence interval:
A (1-α)100% confidence interval for σ2 is
![]()
Note: The sample must be taken from a normally distributed population.
Note #2: If a confidence interval for σ is desired, we can take the square root of each part.
Now that we have the confidence interval formula, let's try a couple examples.
Example 3
Suppose a sample of 30 ECC students are given an IQ test. If the sample has a standard deviation of 12.23 points, find a 90% confidence interval for the population standard deviation.
Solution: We first need to find the critical values:
![]() and
and ![]()
Then the confidence interval is:

So we are 90% confident that the standard deviation of the IQ of ECC students is between 10.10 and 15.65 bpm.
Finding Confidence Intervals Using StatCrunch
Note: If you need a confidence interval about the population standard deviation, take the square root of the values in the resulting confidence interval. |
Here's one for you to try:
Example 4
In Example 3 in Section 9.1, we assumed the standard deviation of the resting heart rates of students was 10 bpm.
| heart rate | ||||
| 61 | 63 | 64 | 65 | 65 |
| 67 | 71 | 72 | 73 | 74 |
| 75 | 77 | 79 | 80 | 81 |
| 82 | 83 | 83 | 84 | 85 |
| 86 | 86 | 89 | 95 | 95 |
(Click here to view the data in a format more easily copied.)
Use StatCrunch to find a 95% confidence interval for the standard deviation of the resting heart rates for students in this particular class.
Using StatCrunch, we get the following result:
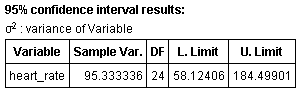
So the standard deviation is between ![]() and
and ![]() .
.
