Section 9.1: Estimating a Population Proportion
Objectives
By the end of this lesson, you will be able to...
- construct and interpret a CI for p
- determine the sample size necessary for estimating p within a specified margin of error
For a quick overview of this section, watch this short video summary:
Perhaps the most common confidence intervals that we see in the news are regarding proportions. Consider the following examples:
Hispanics See Their Situation in U.S. Deteriorating
Half (50%) of all Latinos say that the situation of Latinos in this country is worse now than it was a year ago, according to a new nationwide survey of 2,015 Hispanic adults conducted by the Pew Hispanic Center. [...] The margin of error of the survey is plus or minus 2.8 percentage points at the 95% confidence level. (Source: Pew Research)International Poll: No Consensus On Who Was Behind 9/11
A new WorldPublicOpinion.org poll of 17 nations finds that majorities in only nine of them believe that al Qaeda was behind the 9/11 terrorist attacks on the United States. [...] On average, 46 percent say that al Qaeda was behind the attacks while 15 percent say the US government, seven percent Israel, and seven percent some other perpetrator. One in four say they do not know. [...] Margins of error range from +/-3 to 4 percent. (Source: WorldPublicOpinion)Stem cell, marijuana proposals lead in Mich. poll
A recent poll shows voter support leading opposition for ballot proposals to loosen Michigan's restrictions on embryonic stem cell research and allow medical use of marijuana. The EPIC-MRA poll conducted for The Detroit News and television stations WXYZ, WILX, WOOD and WJRT found 50 percent of likely Michigan voters support the stem cell proposal, 32 percent against and 18 percent undecided. The telephone poll of 602 likely Michigan voters was conducted Sept. 22 through Wednesday. It has a margin of sampling error of plus or minus 4 percentage points. (Source: Associated Press)
In Section 8.2, saw the following excerpt from a report by the Pew Research Foundation:
Hispanics See Their Situation in U.S. Deteriorating
Half (50%) of all Latinos say that the situation of Latinos in this country is worse now than it was a year ago, according to a new nationwide survey of 2,015 Hispanic adults conducted by the Pew Hispanic Center. (Source: Pew Research)
Further down that particular article, there's another interesting line:
The margin of error for the full sample is plus or minus 2.8 percentage points; for registered voters, the margin of error is 4.4 percentage points.
How did they determine that the margin was ±2.8%?
The Logic of Confidence Intervals
The whole point of collecting information from a sample is to gain some information about the population. For example, when the report says that half of all Latinos say that the situation is worse now than it was a year ago, it's not saying that they actually asked every single Latino living in the United States. Rather, it's based on a sample.
In a similar manner, consider one of the results from the American Time Use Survey:
Employed persons worked an average of 7.6 hours on the days that they worked. They worked longer on weekdays than on weekend days - 7.9 versus 5.6 hours.
The news release isn't saying that the average of time spent for all employed persons is 7.6 hours per day - they're referring to those in the sample of 12,250 individuals in the study.
Both of these examples are called point estimates. 50%, for example, is the point estimate for the percentage of all Latinos who feel that way. Similarly, the average number of hours worked per day of 7.6 is a point estimate the average number of hours worked per day for all employed persons.
A confidence interval estimate is an interval of numbers, along with a measure of the likelihood that the interval contains the unknown parameter.
The level of confidence is the expected proportion of intervals that will contain the parameter if a large number of samples is maintained. The notation we use is ![]() for the confidence interval. (This will make more sense a bit later!)
for the confidence interval. (This will make more sense a bit later!)
The idea of a confidence interval is this: Suppose we're wondering what proportion of ECC students are part-time. We might take a sample of 100 individuals and find a sample proportion of 65%. If we say that we're 95% confident that the real proportion is somewhere between 61% and 69%, we're saying that if we were to repeat this with new samples, and gave a margin of ±4% every time, our interval would contain the actual proportion 95% of the time.
See, every time we get a new sample, we have a new estimate, and hence a new confidence interval. Sometimes we'll be right. Sometimes we won't. The idea behind a certain % (like 95%) is that we're saying we'll be right 95% of the time. Here's a visual for 20 theoretical samples and corresponding confidence intervals for the proportion who work:
You can see that 1 of the 20 (5%) confidence intervals doesn't contain the actual value of 68.5% (based on data from elgin.edu). But the other 19 (or 95% of them) do contain the real value.
This is the idea for what we'll be doing. We'll be giving an interval of value for where we think the mean, proportion, or standard deviation is, and then a confidence level for what proportion of the intervals we believe will contain the true parameter.
Exploring Confidence Intervals about the Population Mean
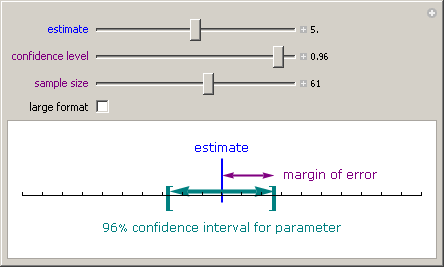
 To do some exploring yourself, go to the Demonstrations Project from Wolfram Research, and download the Confidence Intervals demonstration. If you haven't already, download and install the player by clicking on the image to the right.
To do some exploring yourself, go to the Demonstrations Project from Wolfram Research, and download the Confidence Intervals demonstration. If you haven't already, download and install the player by clicking on the image to the right.
Once you have the player installed and the Confidence Intervals demonstration downloaded, move the sliders for the estimate, confidence level, and sample size on the confidence interval and margin of error.
Even though this is about a confidence interval for the mean (and not the proportion), the idea is the same. Hopefully you noticed a few keys:
- The estimate simply slides the interval left and right.
- A larger confidence level means a wider interval - to be more confident, we need to cast a wider net in order to "catch" the actual population mean.
- A larger sample size means a narrower interval - the more we have in our sample, the closer we are to having the actual population mean.
Constructing Confidence Intervals
Before we can start constructing confidence intervals, we need to review some of the theoretical framework we set up in Chapter 8. In particular, the information about the distribution of ![]() .
.
Reviewing the Distribution of the Sample Proportion
In Section 8.2, we introduced the idea of a proportion, along with its distribution.
Sampling Distribution of 
For a simple random sample of size n such that n≤0.05N (in other words, the sample is less than 5% of the population), and np(1-p)≥10, ![]() is approximately normally distributed, with
is approximately normally distributed, with
![]() and
and 
So if np(1-p)≥10, ![]() will be approximately normally distributed, with the mean and standard deviation above. Using the properties of the normal distribution, that means about 95% of all sample proportions will be within 1.96 standard deviations of the mean (p).
will be approximately normally distributed, with the mean and standard deviation above. Using the properties of the normal distribution, that means about 95% of all sample proportions will be within 1.96 standard deviations of the mean (p).
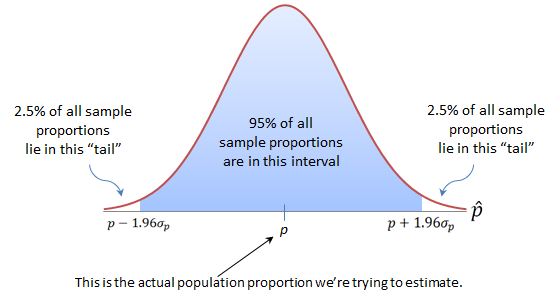
In other words, 95% of all sample proportions will be in the interval:
![]()
With a little algebraic manipulation, we get the following:
![]()
And since  , we can further get the 95% confidence interval for the proportion as:
, we can further get the 95% confidence interval for the proportion as:
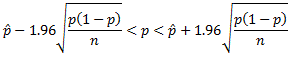
This is a problem, though. How can we say that the population proportion, p, is in this interval, when the lower and upper bounds contain p?! All is not lost! In general, we can say that as long as ![]() and
and ![]() , we can use
, we can use ![]() in place of p in the standard error of the sample proportion, which gives us this for a 95% confidence interval:
in place of p in the standard error of the sample proportion, which gives us this for a 95% confidence interval:
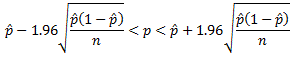
Or rephrased,
So in general, this means that 95% of the time, an interval of that form would contain the population proportion - that's exactly what we want!
Finding a 95% Confidence Interval
Example 1
Polls are very common examples of confidence intervals, so let's look at a controversial topic in Illinois - concealed carry. Illinois was the last state to allow concealed carry in public places, and the issues has been brought up frequently through polling over the years. Two 2011 polls are interesting to consider.
First, a poll sponsered by the Illinois Council Against Handgun Violence conducted March 23-27, 2011 found that 56% of likely voters statewide oppose concealed-carry legislation. Find a 95% confidence interval for the proportion of likely voters who oppose this type of legislation.
Interestingly, another poll conducted at the same time by the Illinois State Rifle Association found that 47% of voters in four state senate districts support concealed carry legislation. Find a 95% confidence interval for the proportion of likely voters who oppose this type of legislation.
Solution:
Before we can do any analysis, we need to consider if we are able to find a confidence interval. To do that, we need the sample sizes for these polls. From the links, we can see that 600 likely voters were included in the first sample, with 957 in the second. In both cases, ![]() and
and ![]() , so we can perform the confidence intervals.
, so we can perform the confidence intervals.
For the ICAHV poll, ![]() = 56%, so a 95% confidence interval is:
= 56%, so a 95% confidence interval is:
So we can be 95% confident that the proportion of likely Illinois voters who oppose concealed carry legislation is between 52% and 60%.
For the ISRA poll, ![]() = 47%, so a 95% confidence interval is:
= 47%, so a 95% confidence interval is:
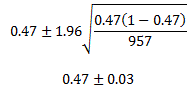
So we can be 95% confident that the proportion of voters in these districts who support concealed carry legislation is between 44% and 50%.
Wait... what is going on? Something is clearly wrong here. If these polls were similar, then they should have opposite results, not relatively similar for the opposite side of the issue!
So what happened? Well, the first issue is the samples - they're not drawn from the same population. Of greater concern is the questioning in the second survey. Look at the link and the question wording in general. What concerns would you have?
Constructing Confidence Intervals about a Population Proportion
What if we want to be more confident? Well, we can just replace the 1.96 with a different Z corresponding to a different area in the "tails". With that, we have the following result:
A (1-α)100% confidence interval for p is
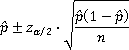
Note: We must have ![]() and
and ![]() in order to construct this interval.
in order to construct this interval.
The Margin of Error
Most of the time (but not always), confidence intervals look roughly like:
point estimate ± margin of error
So in the case of a confidence interval for the population proportion shown above, the margin of error is the portion after the ±, or..
The margin of error, E, in a (1-α)100% confidence interval for p is
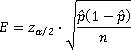
where n is the sample size.
For more on the margin of error, watch this YouTube video, from David Longstreet:
Let's look at one of the polls above and see how they found the margin of error for their confidence interval.
Example 2
Consider the excerpt shown below from a poll conducted by Pew Research:
Stem cell, marijuana proposals lead in Mich. poll
A recent poll shows voter support leading opposition for ballot proposals to loosen Michigan's restrictions on embryonic stem cell research and allow medical use of marijuana. The EPIC-MRA poll conducted for The Detroit News and television stations WXYZ, WILX, WOOD and WJRT found 50 percent of likely Michigan voters support the stem cell proposal, 32 percent against and 18 percent undecided. The telephone poll of 602 likely Michigan voters was conducted Sept. 22 through Wednesday. It has a margin of sampling error of plus or minus 4 percentage points. (Source: Associated Press)
Using the confidence interval formula above, let's see if we can get the ±4% they got.
Since we want a 95% confidence level, α = 0.05. The margin of error is then:
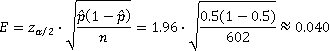
And so the margin of error is ±4.0%.
Why don't you try one:
Example 3
Read the following excerpt and calculate the margin of error for the indicated sample proportion.
Tories lead but voter volatility on the rise
OTTAWA–The Conservatives still hold a strong lead but shifting allegiances in Quebec and a sharp upsurge in ABC (Anybody But Conservative) thinking nationally could put a Tory majority victory out of reach, a new poll shows.
[...]
The Toronto Star/Angus Reid survey, conducted after the televised leaders' debates, shows support for Stephen Harper's Conservative party remains unchanged at 40 per cent, while the Liberals are slightly closing the gap, with their backing among decided voters rising to 25 per cent, according to the survey.
The poll on voting intentions, approval ratings and strategic voting surveyed 1,176 adult Canadians on Oct. 2-3 and has a margin of error of plus-or-minus [xx] percentage points, 19 times out of 20.
The first thing we need is to parse out the information we're given. We can see that the indicated sample proportion is 0.40, with n = 1,176, and the desired confidence interval is 19/20 = 95%.
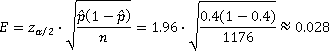
So the margin of error is ±2.8%. You can check to see if the authors of the article agree by reading the original article.
Finding Confidence Intervals Using StatCrunch
With Data
With Summary
* To get the counts, first create a frequency table. If you have a grouping variable, use a contingency table. |
An interesting consequence of margins of errors in polls is the concept of a "statistical tie". Check out the following excerpt from a Wall Street Journal Article:
Financial Crisis Has Little Sway in Presidential Poll
WASHINGTON -- The race between Barack Obama and John McCain remains very tight, despite financial turmoil that has turned the nation's attention to economic issues that tend to favor the Democrats, according to a new Wall Street Journal/NBC News poll.
[...] Overall, the race remains a statistical tie, with 48% favoring Sen. Obama and his running mate, Sen. Joe Biden, and 46% favoring Sen. McCain and his vice-presidential choice, Alaska Gov. Sarah Palin. In the latest Journal poll, two weeks ago, Sen. Obama had a one-point edge. The new poll had a margin of error of plus or minus three percentage points. (Source: Wall Street Journal)
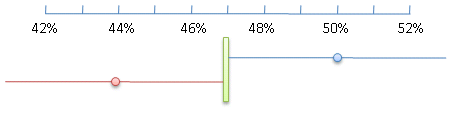
In this case, with a margin of error of ±3%, the confidence intervals actually overlap.

In fact, they'd overlap even if they were 49% and 45%.
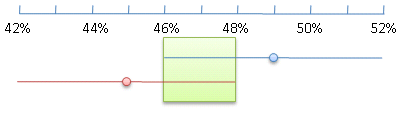
It wouldn't be until 50% and 44% that we could say Obama would be statistically ahead of McCain.
Determining the Sample Size Needed
We sometimes need to know the sample size necessary to get a desired margin of error. The way we answer these types of questions is to go back to the margin of error:
The margin of error, E, in a (1-α)100% confidence interval p is
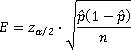
where n is the sample size.
If we're given the margin of error, we can solve for the sample size and get the following result:
The sample size required to obtain a (1-α)100% confidence interval for p with a margin of error E is:
![]()
where n is rounded up to the next integer and ![]() is a prior estimate of p. If no prior estimate is available, use
is a prior estimate of p. If no prior estimate is available, use ![]() = 0.5.
= 0.5.
Let's try one.
Example 4
Suppose you want to know what proportion of Elgin, IL residents are registered to vote. You'd like your results to be accurate to within 2 percentage points with 95% confidence. What sample size is necessary..
- if you use results from the US Census stating that about 72.1% of all citizens were registered for the 2004 election? (Source: US Census)
- you don't use a prior estimate?
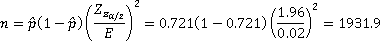
So we would need a sample size of at least 1,932 citizens.
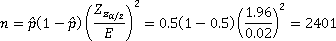
So without the prior estimate, we would need a sample size of at least 2,401 citizens.
We should note here that having the prior estimate saves us from sampling an additional 500 citizens.