Section 9.4: Putting It Together: Which Procedure Do I Use?
Objectives
By the end of this lesson, you will be able to...
- determine the appropriate CI to construct
In this chapter, we've learned three different confidence intervals. In order for them to be of any value, we need to know which one to apply. Let's do a quick review of the three.
Confidence Intervals about p
This is probably the easiest one - whenever we're looking at a proportion (percent), this is the confidence interval we want.
A (1-α)100% confidence interval for p is
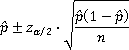
Note: We must have ![]() and
and ![]() in order to construct this interval.
in order to construct this interval.
Confidence Intervals about μ
This is the typical confidence interval for a mean. Use this when you're given information from a sample or if you're only given data. (In that case, you calculate the sample mean and standard deviation yourself, so you can't possibly know the population standard deviation.)
In general, a (1-α)100% confidence interval for μ when σ is unknown is
![]()
where ![]() is computed with n-1 degrees of freedom.
is computed with n-1 degrees of freedom.
Note: The sample size must be large (n≥30) or the population must be normally distributed.
Confidence Intervals about σ2 and σ
The last confidence interval is for either the variance or standard deviation. You should be able to key on those words to help you recognize this confidence interval.
A (1-α)100% confidence interval for σ2 is
![]()
Note: The sample must be taken from a normally distributed population.
Some Examples
Let's try some examples. For each situation, simply determine which confidence interval should be used. You shoud specify the parameter and state the appropriate interval formula (because there are two for the population mean).
Example 1
We would like to know the fraction of ECC students who commute to school from their parents' homes. We send emails to students using their ECC email account until 100 have responded; 62 of the responders were commuters.
Find a 95% confidence interval for the fraction of ECC students who commute to school from their parents' homes.
Even though the word fraction is used here, this is a confidence interval for the population proportion. The appropriate formula would be:
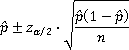
Example 2
Suppose a student measuring the boiling temperature of a certain liquid observes the readings (in °C) 102.5, 101.7, 103.1, 100.9, 100.5, and 102.2 on 6 different samples of the liquid. He calculates the sample mean to be 101.82. If he knows that the standard deviation for this procedure is 1.2°, what is the confidence interval for the population mean at a 95% confidence level?
The problem clearly states that we're finding a confidence interval for the population mean. We're also told that the student knows the standard deviation for this procedure is 1.2°. The implication in this statement is that the 1.2° is the standard deviation for all experiments of this type - the population standard deviation.
The confidence interval we should use, then, is:
![]()
Example 3
To assess scholastic performance, a state administers an achievement test to a simple random sample of 100 high school seniors. The mean score of the students who took the exam is 99.7 points, with a standard deviation of 7.9 points. Find an approximate 90% confidence interval for the average of the population scores that would have been obtained had every high school senior in the state been administered the achievement test.
Since we're asked to find a confidence interval for the average of the population scores, this is a confidence interval for the population mean.
The wording is a bit unclear, but the key phrase is the following: The mean score of the students who took the exam is 99.7 points, with a standard deviation of 7.9 points. The implication here is that the 7.9 is the standard deviation of the sample, not the entire population. The confidence interval we should use is thus:
![]()
Example 4
We know from previous examples that the standard deviation of IQs is normally distributed with a standard deviation of 15. Suppose we wonder if the IQs of ECC students have more variation. To answer this question, we collect the IQs from a random sample of ECC students and find a standard deviation of 16.2.
Based on this information, do you believe with 95% confidence that the IQs of ECC students have more variation than the population?
The problem is talking about variation, which always implies variance or standard deviation. Also, we're given the standard deviation of the sample, which also implies that this is a confidence interval for the population standard deviation.
![]()
