Section 8.2: Distribution of the Sample Proportion

Objectives

By the end of this lesson, you will be able to...

describe the sampling distribution of a sample proportion
compute probabilities of a sample proportion

For a quick overview of this section, watch this short video summary:

The Sample Proportion

Consider these recent headlines:

Hispanics See Their Situation in U.S. Deteriorating
Half (50%) of all Latinos say that the situation of Latinos in this country is worse now than it was a year ago, according to a new nationwide survey of 2,015 Hispanic adults conducted by the Pew Hispanic Center. (Source: Pew Research)

Automatic enrollment in 401(k) doesn't take care of everything
Never got around to signing up for the company retirement plan? The boss may have done it for you. Forty-two percent of employers with 401(k) plans automatically enroll new or existing employees in the plans, nearly double the 23 percent from 2006, according to estimates from the 2008 401(k) Benchmarking Survey by the International Foundation of Employee Benefit Plans and Deloitte Consulting. The survey polled 436 employers with workforces of all sizes. (Source: Chicago Tribune)

Stem cell, marijuana proposals lead in Mich. poll
A recent poll shows voter support leading opposition for ballot proposals to loosen Michigan's restrictions on embryonic stem cell research and allow medical use of marijuana. The EPIC-MRA poll conducted for The Detroit News and television stations WXYZ, WILX, WOOD and WJRT found 50 percent of likely Michigan voters support the stem cell proposal, 32 percent against and 18 percent undecided. (Source: Associated Press)

These three articles all have something in common - they're referring to sample proportions - 50% of all Latinos, 42% of employers, and 50% of likely Michigan voters, respectively, in the three articles above. Proportions are the number with that certain characteristics divided by the sample size.

In general, if we let x = the number with the specific characteristic, then the sample proportion, , (read "p-hat") is given by:

Where is an estimate for the population proportion, p.

Let's focus for a bit on x, the number with that characteristic. If we rephrase that a bit, and consider an individual having that characteristic as a "success", we can see that x follows the binomial distribution.

From Section 6.2, we know that the distribution of a binomial random variable becomes bell-shaped as n increases. The three histograms below demonstrate the effect of the sample size on the distribution shape.

n=10, p=0.8

n=20, p=0.8

n=50, p=0.8

As the number of trials in a binomial experiment increases, the probability distribution becomes bell-shaped. As a rule of thumb, if np(1-p)≥10, the distribution will be approximately bell-shaped.

With our new knowledge of the normal distribution, it appears that if np(1-p)≥10, x is normally distributed, which implies that is as well. All we need to know, then, is its mean and standard deviation.

Sampling Distribution of

For a simple random sample of size n such that n≤0.05N (in other words, the sample is less than 5% of the population),

The shape of the sampling distribution of is approximately normal provided
np(1-p)≥10
The mean of the sampling distribution of is .
The standard deviation of the sampling distribution of is

Now that we know how is distributed, we can use that information to find some probabilities.

Let's see a couple examples.

Example 1

In a typical class, about 70% of students receive a C or better. Out of a random sample of 100 students, what is the probability that less than 60 receive a C or better?

Solution:

Since there are millions of students, 100 is definitely less than 5% of the population.

Because , we can say that the distribution of is normal.

We then need to find the mean and standard deviation. From the distribution of the sample proportion, we know

standard deviation

Using StatCrunch, the probability of observing a sample proportion of less than 60/100 = 0.6 is

StatCrunch calculation

So the probability of observing less than 60 out of 100 students is about 0.015 - pretty unusual.

Example 2

Source: stock.xchng

A basketball player traditionally makes 85% of her free throws. Suppose she shoots 100 free-throws during practice. Would it be unusual for her to make less than 75?

Solution:

Since our player can shoot an unlimited number of free throws, we can assume that 100 is less than 5% of the population. Checking the distribution:

So the distribution should be normally distributed, with mean and standard deviation

standard deviation

Using StatCrunch, with p = 75/100 = 0.75:

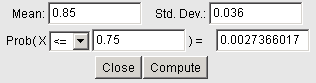
StatCrunch calculation

So the probability that she makes less than 75 out of 100 is about 0.0027. That means she'll make less than 75 out of 100 about 0.27% of the time, which is very unusual.

Here's one for you to try:

Example 3

According to data from the American Cancer Society, about 3.86% of women develop breast cancer between the ages of 40-59.

What is the probability that in a random sample of 500 39-year-old women without breast cancer, more than 20 will develop breast cancer by the age of 60?

[ reveal answer ]

Since there are about 2 million women aged 39 in the United States, the sample size of 500 is definitely less than 5% of the population. Checking the distribution:

So the distribution should be approximately normal, with mean and standard deviation

standard deviation

Using StatCrunch, the probability of observing a sample proportion of 20/500 = 0.04 or more is:

StatCrunch calculation

So there's a probability of about 0.435 that more than 20 of the 500 39-year-old women will develop breast cancer by age 60.

A note on rounding: We've already seen that rounding is an important topic in this course. In this particular section, rounding can make a significant difference in your calculations. It's important that you take a minute and watch this video regarding the effect of rounding when doing the calculations from this section: The Dangers of Rounding (Quicktime or iPod)