Section 5.6: Putting It Together: Which Method Do I Use?

Objectives

By the end of this lesson, you will be able to...

determine the appropriate probability rule to use
determine the appropriate counting technique to use

The last thing we really need to do is connect all these counting techniques to the stated purpose - probability. We'll start by first focusing on choosing the correct probability rule. Once we have that down, we'll continue to the next stage of selecting the correct counting technique.

Probability Rules

Let's start by reviewing the probability rules from the previous sections.

The Basic Principle of Probability (Classical Method)

P(E) =	number of ways E can occur	=	N(E)
	total number of possible outcomes		N(S)

The General Addition Rule

P(E or F) = P(E) + P(F) - P(E and F)

The Complement Rule

P(E) + P(E^c) = 1

General Multiplication Rule

The probability that two events E and F both occur is

P(E and F) = P(E) • P(F|E)

Our task then, is choosing the correct rule. Here's a decision-making flowchart:

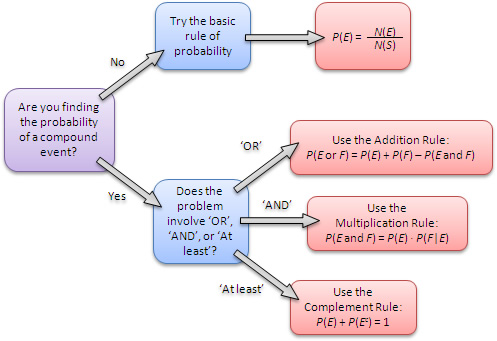
probability rules flowchart

Let's try an example together.

Example 1

Problem: Suppose a basketball player makes 80% of her free throws. If she shoots five free throws, find the probability that she makes at least one basket.

Solution: Let's try following our flowchart:

Are you finding the probability of a compound event?
Yes.
Does the problem involve 'AND', 'OR', or 'At least'?
At least.
Use the Complement Rule.

The Complement Rule is P(E) + P(E^c) = 1. In our case, we have something like this:

P(she makes at least one) + P(she misses all five) = 1

We can find what we want by solving for it:

P(she makes at least one) = 1 - P(she misses all five)

Now, we need to look at the probability that she misses all five. Let's try the sequence again:

Are you finding the probability of a compound event?
Yes.
Does the problem involve 'AND', 'OR', or 'At least'?
AND. (We want the probability that she misses the first and the second and the third, etc)
Use the Multiplication Rule.

If we assume the individual attempts are independent (granted, a big assumption), we can find the probability that she misses all five by multiplying the probability that she misses one by itself five times.

P(she makes at least one)
= 1 - P(she misses all five)
= 1 - (0.2)(0.2)(0.2)(0.2)(0.2)
=0.99968

So she'll make at least one basket 99.97% of the time!

All right, it's time for you to try some yourself. Here we go...

Example 2

Consider a standard 52-card deck of playing cards. A single card is drawn at random, with the following events defined:

A = a diamond is drawn
B = a face card is drawn (face cards are Jacks, Queens, or Kings)

Find P(A or B).

[ reveal answer ]

OK, so this one was a bit easy. It clearly says "Find P(A or B)." So we need the Addition Rule:

P(A or B) = P(A) + P(B) - P(A and B)

If you're interested in the solution, it would be:

P(A or B)
= P(diamond) + P(face) - P(diamond face)
= 13/52 + 12/52 - 3/52 = 22/52 = 11/26

Example 3

Suppose a fair die is tossed and a fair coin is flipped. Find the probability that the die is even and the coin is heads.

[ reveal answer ]

Following our flowchart, we have this sequence:

Are you finding the probability of a compound event?
Yes.
Does the problem involve 'AND', 'OR', or 'At least'?
AND.
Use the Multiplication Rule.

The key here is the word and in the last sentence: "Find the probability that the die is even and the coin is heads."

With that in mind, we use the Multiplication Rule:

P(E and F) = P(E) • P(F|E)
= P(die is even) • P(heads | die is even)
= (3/6) • (1/2) = 3/12 = 1/4

Note: Since the die and coin are independent, P(F|E) = P(F). Whether the die is even certainly doesn't affect whether the coin is heads or tails!

Example 4

Source: stock.xchng

Texas Hold'Em is form of poker regaining popularity recently due to the exposure of the World Series of Poker on ESPN. The game is fairly complex, but components of it can be relatively easy to understand.

From Wikipedia
Hold 'em is a community card game where each player may use any combination of the five community cards and the player's own two hole cards to make a poker hand, in contrast to poker variants like stud or draw where each player holds a separate individual hand.

The game is played by first dealing every player two cards. Then three card are dealt face-up in the middle of the table (this is called the flop). All players are allowed to use these "community" cards in the middle of the table along with the two best . Later, two more card are dealt, with a total of five "community" cards for all players to use in their hands.

Suppose you are dealt A♥Q♥. If we assume the other 50 cards are all equally likely to be dealt during the flop, what is the probability that the next three cards are also hearts, giving you a flush (five of the same suit) after the flop?

Just focus on choosing the correct probability rule - don't worry about actually finding the probability.

[ reveal answer ]

There's a bit of terminology here, so let's look at the situation. We currently have A♥Q♥. Three cards are going to be dealt from the remaining 50 cards. Following our flowchart:

Are you finding the probability of a compound event?
No.
Try the basic rule of probability.

In this case, that rule translates to something like the following:

P(flush) =	number of ways to get three more hearts
	total number of ways to deal 3 cards

We'll worry about how to count these in the next section.

Once you've determined which probability rule to apply, you often need some counting techniques in order to complete the problem. For many students, this aspect of probability questions is the most troublesome. Like the previous page (and your text), we'll illustrate the main ideas with a flow chart.

The Counting Techniques

As with the probability rules, we need to first review some of our different counting techniques, beginning with the most important.

Multiplication Rule of Counting

If a task consists of a sequence of choices in which there are p ways to make the first choice, q ways to make the second, etc., then the task can be done in

p•q•r•...

different ways.

Permutations of n Distinct Objects Taken r at a Time

The number of arrangements of r objects chosen from n objects in which

the n objects are distinct,
repeats are not allowed,
order matters,

is given by the formula .

Combinations of n Distinct Objects Taken r at a Time

The number of arrangements of n objects using r≤n of them, in which

the n objects are distinct,
repeats are not allowed,
order does not matter,

is given by the formula .

Permutations with Non-distinct Items

The number of permutations of n objects, where there are n1 of the 1st type, n2 of the 2nd type, etc, is

Choosing the Appropriate Counting Technique

The trouble, then, becomes choosing which one of these (or more than one) applies to a particular problem.

As we did with the probability rules, we'll illustrate this with a decision-making flowchart. In this case, it's the same one that's in your text.

counting rules flowchart

Let's try one example together.

Example 5

Questions: In the Powerball lottery, there are 5 balls numbered 1-55, and an additional "powerball" numbered 1-42. To win the grand prize, you must match all 5 and the powerball. What is the probability of winning the grand prize with one ticket?

Solutions: To answer this question, we need to remember the basic probability rule. Expanded for this example, it would be something like this:

P(winning) =	number of ways to win
	total number of possible outcomes

The number of ways to win is easy - there's only one!

For the total number of possible outcomes, let's consider our flowchart.

Are we making a sequence of choices?
Yes. We're first counting the number of ways for the 5 balls to be drawn, and then we need to count the number of ways for the powerball to be drawn.
Are the choices independent of each other? (In other words, is the powerball independent of what happens in the first 5 balls?)
Yes.
Use the Multiplication Rule of Counting.

So we need to multiply the number of ways to do each step.

total # of outcomes
= (# of ways for the 5 to be drawn)•(# of ways for powerball)

Since order doesn't matter for the 5 balls, that part is a combination of 5 from 55. The powerball is simply 42, since there are 42 choices.

The total number of outcomes is thus ₅₅C₅•42 = 146,107,962.

The probability is then 1/146,107,962 ≈ 0.000 000 007

That means a $1 ticket has only about a 1 in 150 million chance of winning the grand prize!

Here are some examples to try. Some are counting questions and some are actual probability questions, but the probability rule shouldn't be the hard part. (Hint: They can all use the classical method!)

Example 6

Suppose you are told to create a password that has the following rules:

it must consist of exactly 4 characters,
one must be a number,
one must be a capitalized, and
the letters must all differ.

How many possible passwords are there following these rules?

[ reveal answer ]

OK, this is a pretty tricky one. Let's follow the flowchart:

Are we making a sequence of choices?
Yes.

choose a spot for the number
choose a spot for the capital letter
choose a number
choose the capital letter
choose the two other letters

Are the choices independent of each other?
No.
Try a tree diagram.

Well, this would be a pretty nasty tree diagram. Let's instead consider the choices we have to make.

choose a spot for the number - there are 4 options for this step
choose a spot for the capital letter - only 3 spots remain
choose a number - there are 10 digits 0-9
choose the capital letter - there are 26 letters
choose the two other letters - since there are only 25 letters remaining, and they cannot repeat, there are 25•24 choices remaining

Our total count is then 4•3•10•26•25•24 = 1,872,000 possible passwords.

Example 7

Suppose you have a bag of 20 blue marbles and 40 red marbles. What is the probability that if 5 are drawn without replacement, 2 are blue and 3 are red?

[ reveal answer ]

We should be able to see that the probability rule is just the basic probability rule:

P(2B & 3R) =	number of ways to draw 2B & 3R
	total number of ways to draw 5 marbles

Following our flowchart when considering the numerator, we get this sequence:

Are we making a sequence of choices?
Sort of. All 5 marbles are drawn at once, so it's not a sequence, but we do have two separate choices. Let's continue on considering only the two blue marbles.
Does order matter?
No. The balls are simply drawn - they're not in a particular order.

So it looks like we should be using a combination. When looking at the entire numerator, we can consider the red and blue marbles to be two choices, and we can multiply the number of ways to draw 2 blue marbles by the number of ways to draw 3 red marbles.

Our probability is then:

P(2B & 3R) =	₂₀C₂•₄₀C₃	≈ 0.3437
	₆₀C₅

Example 8

Source: stock.xchng

In Example 4, you worked on choosing the correct probability rule for a Texas Hold'Em situation. Use your rule to actually calculate the probability. Here's the problem again:

[ reveal answer ]

From Example 12, we know the basic probability rule is:

P(flush) =	number of ways to get three more hearts
	total number of ways to deal 3 cards

Following our flowchart for either the numerator or denominator, we get:

Are we making a sequence of choices?
No. Even though the three cards would be dealt sequentially during an actual game, we can consider them being delivered all at once.
Does order matter?
No. In a card game, the order of the cards in your hand does not matter.

It looks like we again have a combination. In this case, we want to choose 3 of the 11 remaining hearts in the numerator, and 3 of the remaining 50 cards in the denominator.

P(flush) =	₁₁C₃	≈ 0.0084
	₅₀C₃

Note: In case you're wondering about the other players (which is a good question), we typically consider that those players' cards are also randomly distributed. So even though there may actually be less than 50 cards remaining in the dealer's hand, the cards in his or her hand and the cards in your opponents' hands are all randomly distributed, so we consider all 50 to be included with the dealer.