Section 5.2: The Addition Rule and Complements

The Additional Rule for Disjoint Events

We're going to have quite a few rules in this chapter about probability, but we'll start small. The first situation we want to look at is when two events have no outcomes in common. We call events like this disjoint events.

Two events are disjoint if they have no outcomes in common. (Also commonly known as mutually exclusive events.)

Back in 1881, John Venn developed a great way to visualize sets. As is often the case in mathematics, the diagrams took on his name and have since taken on his name - Venn diagrams. Because events are sets of outcomes, it works well to visualize probability as well. Here's an example of a Venn diagram showing two disjoint outcomes, E and F.

Let's continue this a little further and put points on the chart like this -- to indicate outcomes.

Looking at the picture, we can clearly see that P(E) = 5/15 = 1/3, since there are 5 outcomes in E, and 15 total outcomes. Similarly, P(F) also is 1/3.

Next, we want to consider all of the events that are in either E or F. In probability, we call that event E or F. So in our example, P(E or F) = 10/15 = 2/3.

But, we could just see that from the picture! Just count the dots that are E and add to it the number of dots in F.

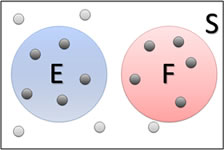
In general, we can create a rule. We'll call it...

Of course, there are often cases when two events do have outcomes in common, so we'll need a more robust rule for that case.

 

General Addition Rule

What happens when two events do have outcomes in common? Well, let's consider the example below. In this case, P(E) = 4/10 = 2/5, and P(F) = 5/10 = 1/2, but P(E or F) isn't 9/10. Can you see why?

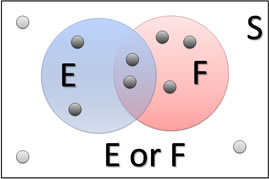
The key here is the two outcomes in the middle where E and F overlap. Officially, we call this region the event E and F. It's all the outcomes that are in both E and F. In our visual example:

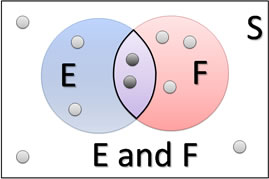
In this case, to find P(E or F), we'll need to add up the outcomes in E with the outcomes in F, and then subtract the duplicates we counted that are in E and F. We call this the General Addition Rule.

Let's try a couple quick examples.

So the key idea and the difference between these two examples - when you're finding
P(E or F), be sure to look for outcomes that E and F have in common.

The Complement Rule

I think the best way to introduce the last idea in this section is to consider an example. Let's look at a deck of standard playing cards again:

And let's define event E = a card less than a King is drawn. If I ask you to find P(E), you're not going to count them up. (You weren't going to, were you?!) No - you'll say there are 52 cards all together, and there are 4 kings, so therefore there must be 48 cards less than a King. So P(E) = 48/52 = 12/13.

The idea that you're already using there is called the complement. (That's complement, with an e. Not compliment, as in "My, you look pretty today!")

The complement of E, denoted E^c, is all outcomes in the sample space that are not in E.

So essentially, the complement of E is everything but the outcomes in E. In fact, some texts actually write it as "not E".

How is the complement helpful? Well, you actually already used the key idea in the example above. Let's look at a Venn diagram.

From Section 5.1, we know that P(S) = 1. Clearly, E and E^c are disjoint, so
P(E or E^c) = P(E) + P(E^c) . Combining those two facts, we get:

Keep this in mind when you're looking at an event that's fairly complicated. Sometimes it's much easier to find the probability of the complement.

 

<< previous section | next section >>

1 2 3 4 5 6 7 8 9 10 11 12 13

This work is licensed under a Creative Commons License.