Section 5.5: Counting Techniques
Objectives
By the end of this lesson, you will be able to...
- solve counting problems using the Multiplication Rule
- solve counting problems using permutations
- solve counting problems using combinations
- solve counting problems involving permutations with non-distinct items
- compute probabilities involving permutations and combinations
For a quick overview of this section, watch this short video summary:
Do you remember the classical method for calculating probabilities from Section 5.1?
| P(E) = | number of ways E can occur | = | N(E) |
| total number of possible outcomes | N(S) |
Well, sometimes counting the "number of ways E can occur" or the "total number of possible outcomes" can be fairly complicated. In this section, we'll learn several counting techniques, which will help us calculate some of the more complicated probabilities.
The Multiplication Rule of Counting
Let's suppose you're preparing for a wedding, and you need to pick out tuxedos for the groomsmen. Men's Tuxedo Warehouse has a Build-A-Tux feature which allows you to look at certain combinations and build your tuxedo online. Let's suppose you have the components narrowed down to two jackets, two vest and tie combinations, and three shirt colors. How many total combinations might there be?
A good way to help understand this type of situation is something called a tree diagram. We begin with the jacket choices, and then each jacket "branches" out into the two vest and tie combinations, and then each of those then "branches" out into the three shirt combinations. It might look something like this:
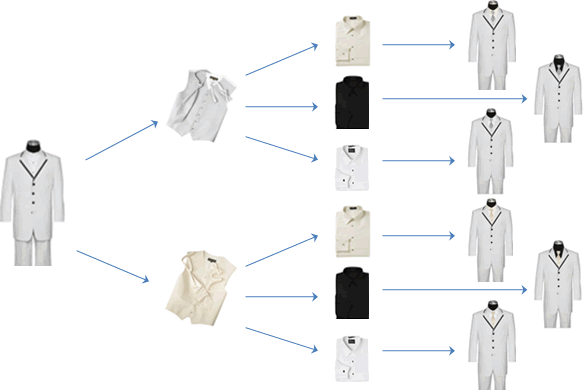
In total, it looks like we have 12 possible combinations of jackets, vests, and shirts. (Of course, some may not fit your fashion sense, but that's another question all-together...)
Isn't there an easier way to do this? Why yes, there is! Think of it this way, for each jacket choice, there are two vest and tie choices. That gives us 4 total jacket and vest/tie combinations. Then, for each of those, there are three shirt choices, giving us a total of 12.
In general, we multiply the number of ways to make each choice, so...
total number of outfits = (number of jackets)•(number of vest/ties)•(number of shirts)
That leads us to the Multiplication Rule of Counting:
Multiplication Rule of Counting
If a task consists of a sequence of choices in which there are p ways to make the first choice, q ways to make the second, etc., then the task can be done in
p•q•r•...
different ways.
Let's try some examples.
Example 1
How many 7-character license plates are possible if the first three characters must be letters, the last four must be digits 0-9, and repeated characters are allowed?
The total number of license plates would be:
(# choices for 1st character)•(# choices for 2nd)•etc..
= 26•26•26•10•10•10•10 = 175,760,000
Example 2
Many garage doors have remote-access keypads outside the door. Let's suppose a thief approaches a particular garage and notices that four particular numbers are well-used. If we assume the code uses all four numbers exactly once, how many 4-digit codes does the thief have to try?
Not very many!
total # of codes = (# choices for 1st digit)•(# for 2nd)•etc...
= 4•3•2•1 = 24
Notice that the number of choices decreased by one for each digit, since the four numbers were used only once. You'll often see this described either as the number are chosen "without replacement" or that "repeats are not allowed".
Example 2, from earlier this section is an example of particular counting technique called a permutation. Rather than giving you formulas and examples myself, I'd like to make another reference to some content from one of my favorite web sites, BetterExplained. Here's what the author, Kalid Azad writes about permutations:
Permutations: The hairy details
Let’s start with permutations, or all possible ways of doing something. We’re using the fancy-pants term “permutation”, so we’re going to care about every last detail, including the order of items. Let’s say we have 8 people:
- Alice
- Bob
- Charlie
- David
- Eve
- Frank
- George
- Horatio
How many ways can we pick a Gold, Silver, and Bronze medal for “Best friend in the world”?
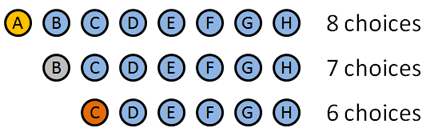
We’re going to use permutations since the order we hand out these medals matter. Here’s how it breaks down:
- Gold medal: 8 choices: A B C D E F G H (Clever how I made the names match up with letters, eh?). Let’s say A wins the Gold.
- Silver medal: 7 choices: B C D E F G H. Let’s say B wins the silver.
- Bronze medal: 6 choices: C D E F G H. Let’s say… C wins the bronze.
We picked certain people to win, but the details don’t matter: we had 8 choices at first, then 7, then 6. The total number of options was 8 * 7 * 6 = 336.
Let’s look at the details. We had to order 3 people out of 8. To do this, we started with all options (8) then took them away one at a time (7, then 6) until we ran out of medals.
We know the factorial is: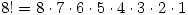 
Unfortunately, that does too much! We only want 8 * 7 * 6. How can we “stop” the factorial at 5?
This is where permutations get cool: notice how we want to get rid of 5*4*3*2*1. What’s another name for this? 5 factorial!
So, if we do 8!/5! we get:
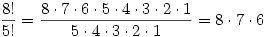
And why did we use the number 5? Because it was left over after we picked 3 medals from 8. So, a better way to write this would be:
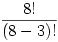
where 8!/(8-3)! is just a fancy way of saying “Use the first 3 numbers of 8!”. If we have n items total and want to pick k in a certain order, we get:
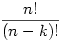just means “Use the first k numbers of n!”
And this is the fancy permutation formula: You have n items and want to find the number of ways k items can be ordered:
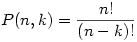
Source: BetterExplained,
Kalid Azad
Article: Easy Permutations and Combinations
Used with permission.
As a side note, many textbooks use the notation nPk rather than Kalid's P(n,k). I've seen both used, though the later tends to be more prevalent in higher-level math classes. We'll stick with the version below, but both are widely accepted.
Permutations of n Distinct Objects Taken r at a Time
The number of arrangements of r objects chosen from n objects in which
- the n objects are distinct,
- repeats are not allowed,
- order matters,
is given by the formula 
.
OK, let's try a couple.
Example 3
Suppose an organization elects its officers from a board of trustees. If there are 30 trustees, how many possible ways could the board elect a president, vice-president, secretary, and treasurer?
In this example, we have 30 "items" (trustees), from which we're choosing 4. Using the notation from your text, we want to calculate 30P4, or
| 30P4 = | 30! | = | 30! | = 30•29•28•27 = 657,720 |
| (30-4)! | 26! |
Example 4
Suppose you're given a list of 100 desserts and asked to rank your top 3. How many possible "top 3" lists are there?
| 100P3 = | 100! | = | 100! | = 100•99•98 = 970,200 |
| (100-3)! | 97! |
In the previous page, we talked about the number of ways to choose k objects from n if the ordered mattered - like giving medals, electing officers, or pickling favorite desserts. What if order doesn't matter, like picking members of a committee?
Again, I'll let Kalid Azad explain.
Combinations, Ho!
Combinations are easy going. Order doesn’t matter. You can mix it up and it looks the same. Let’s say I’m a cheapskate and can’t afford separate Gold, Silver and Bronze medals. In fact, I can only afford empty tin cans.
How many ways can I give 3 tin cans to 8 people?
Well, in this case, the order we pick people doesn’t matter. If I give a can to Alice, Bob and then Charlie, it’s the same as giving to Charlie, Alice and then Bob. Either way, they’re going to be equally disappointed.
This raises and interesting point — we’ve got some redundancies here. Alice Bob Charlie = Charlie Bob Alice. For a moment, let’s just figure out how many ways we can rearrange 3 people.
Well, we have 3 choices for the first person, 2 for the second, and only 1 for the last. So we have 3 * 2 * 1 ways to re-arrange 3 people.
Wait a minute… this is looking a bit like a permutation! You tricked me!
Indeed I did. If you have N people and you want to know how many arrangements there are for all of them, it’s just N factorial or N!
So, if we have 3 tin cans to give away, there are 3! or 6 variations for every choice we pick. If we want to figure out how many combinations we have, we just create all the permutations and divide by all the redundancies. In our case, we get 336 permutations (from above), and we divide by the 6 redundancies for each permutation and get 336/6 = 56.
The general formula is
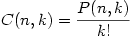
which means “Find all the ways to pick k people from n, and divide by the k! variants”. Writing this out, we get our combination formula, or the number of ways to combine k items from a set of n:
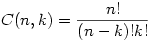
Source: BetterExplained,
Kalid Azad
Article: Easy Permutations and Combinations
Used with permission.
As a side note, many textbooks uses the notation nCk rather than Kalid's C(n,k). As with permutations, we'll stick with the version below, but both are widely accepted.
Combinations of n Distinct Objects Taken r at a Time
The number of arrangements of n objects using r≤n of them, in which
- the n objects are distinct,
- repeats are not allowed,
- order does not matter,
is given by the formula 
.
All right, let's try this new one out.
Example 5
Let's consider again the board of trustees with 30 members. In how many ways could the board elect four members for the finance committee?
In this example, we have 30 "items" (trustees), from which we're choosing 4. Unlike in Example 3, order doesn't matter for this example, so we're looking at a combination rather than a permutation.
| 30C4 = | 30! | = | 30! | = | 30•29•28•27 | = 27,405 |
| (30-4)!•4! | 26!4! | 4•3•2•1 |
You may notice that this number is quite a bit smaller than in Example 3. The reason is that we don't care about order now, so electing trustees A, B, C, and D for the committee is no different than electing trustees B, C, A, and D. That's different than in Example 3, where we were electing them to particular positions.
Example 6
Suppose you're a volleyball tournament organizer. There are 10 teams signed up for the tournament, and it seems like a good idea for each team to play every other team in a "round robin" setting, before advancing to the playoffs. How many games are possible if each team plays every other team once?
This may not initially seem like a combination, but let's take closer look. We have 10 "items" (teams) from which we're choosing 2. We don't care about order, since team A playing team B is the same as team B playing team A. That's exactly a combination!
| 10C2 = | 10! | = | 10! | = | 10•9 | = 45 |
| (10-2)!•2! | 8!2! | 2•1 |
Wow, that's a lot of games! That's why most tournaments go with a "pool" structure and split the tournament up into two "pools" of 5.
You can see more on the "round robin" structure for tournaments at Wikipedia.
This second type is less common. What if we want to know how many ways to order n objects, but they're not all distinct? Here's an example to illustrate:
Example 7
In how many ways could the letters in the word STATISTICS be rearranged?
The answer is a little tricky. Think of the rearranged words as places for letters to go. Something like this:
In STATISTICS, we have the following letters:
3 S's
3 T's
2 I's
1 A
1 C
We can't really say that there are 4 choices for the first letter and proceed from there, since the number of choices for the second letter depend on which letter was chosen for the first.
Instead, we choose the spots for each of the letters. First, pick 3 of the 10 spots for the S's. We can do that in 10C3 ways. Then pick 3 spots for the 3 T's. We can do that in 7C3 ways. Similarly, we can pick the spots for the I's, the A, and the C in 4C2, 2C1, and 1C1 ways, respectively. In total, that means we rearrange the letters in:
10C3•7C3•4C2•2C1•1C1 ways
It may just be me, that is really messy. Oddly enough, writing out the combinations reveals a nice way to simplify it:
| 10! | • | 7! | • | 4! | • | 2! | • | 1! | = | 10! |
| 7!•3! | 4!•3! | 2!•2! | 1!•1! | 1!•0! | 3!•3!•2!•1!•1! |
Permutations with Non-distinct Items
The number of permutations of n objects, where there are n1 of the 1st type, n2 of the 2nd type, etc, is
One quick example:
Example 8
In how many ways can the word REARRANGE be rearranged?
Wittiness aside, this is the same as the previous example. In this case, we have 3 R's, 2 A's, 2 E's, 1 N and 1 G. The total number of permutations is thus:
| 9! | = 15,120 |
| 3!•2!•2!•1!•1! |
This work is licensed under a Creative
Commons License.