Section 5.4: Conditional Probability and the General Multiplication Rule

Objectives

By the end of this lesson, you will be able to...

compute conditional probabilities
use the General Multiplication Rule
determine the independence of events

For an overview probability, watch this video:

Conditional Probability

Remember in Example 3, in Section 5.3, about rolling two dice? In that example, we said that events E (the first die is a 3) and F (the second die is a 3) were independent, because the occurrence of E didn't effect the probability of F. Well, that won't always be the case, which leads us to another type of probability called conditional probability.

Conditional Probability

The notation P(F|E) is read "the probability of F given E" and represent the probability that event F occurs, given that event E has already occurred.

Let's look again at Example 1 from that same section.

Example 1

Consider the experiment where two cards are drawn without replacement. (Without replacement means one is drawn and then the second is drawn without putting the first one back.) Define events E and F this way:

E = the first card drawn is a King

F = the second card drawn is a King

Find P(F|E).

[reveal answer]

P(F|E) is the probability that the second card is a king given if the first card drawn was a king. In that case, there will be 3 kings left out of 51 cards, so

P(F|E) = 3/51

It can be helpful again to look at a Venn diagram to illustrate the idea. Let's look at this one that we used back in section 5.2.

Example 2

Venn diagram

Find P(E|F).

[reveal answer]

OK, this is a little trickier. P(E|F) is the probability that event E occurs given that event F has already occurred. Let's change the image a bit. Since F has occurred, we can focus on just those "outcomes" in F.

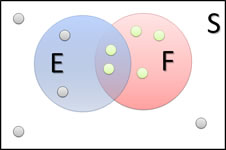
Venn diagram

And then of those, we want the probability that the "outcome" is in E. Since there are 2 of those in E, and 5 total,

P(E|F) = 2/5.

One more example.

Example 3

Let's consider a survey given to 52 students in a Basic Algebra course at ECC, with the following responses to the statement "I enjoy math."

	Strongly Agree	Agree	Neutral	Disagree	Strongly Disagree	Total
Male	6	10	3	0	0	19
Female	8	14	7	4	0	33
Total	14	24	10	4	0	52

What is the probability that a student enjoys math (Agree or Strongly Agree) given that the student is a female?

[reveal answer]

There are 33 female students total. Of those, 22 responded that they enjoyed math, so...

P(enjoys math | female) = 22/33 = 2/3

The Monty Hall Problem

An interesting example of conditional probability is the classic Monty Hall Problem. This is based on an old game show, where the host would show three doors. Behind one was a new car, and behind the others were goats. The twist was, once you made your choice, Monty would open one of the other doors showing a goat. The question then - should you switch? The answer is different from what you would think. Here's another video from Clive Rix at the University of Leicester in Leicester, England:

Don't believe it? Try this interactive feature from the New York Times, or watch this video from the show Numb3rs.

Wow - you never know where conditional probability can be applied!

The General Multiplication Rule

Let's look again at the experiment from Example 1 in Section 5.3.

Example 4

Source: stock.xchng

E = the first card drawn is a King

F = the second card drawn is a King

How would we find P(E and F)?

We know from Example 1 that E and F are not independent, so we know we can't use the Multiplication Rule for Independent Events. It's probably not too difficult to see how we might do it, though.

P(E and F)	= P(first is King and second is King)
	= P(first is King)•P(second is King given first is King)
	= (4/52)(3/51)
	≈ 0.0045

Or in other words, P(E and F) = P(E) • P(F|E)

This idea is actually a version of the Multiplication Rule for Independent Events, and is called the General Multiplication Rule.

General Multiplication Rule

The probability that two events E and F both occur is

P(E and F) = P(E) • P(F|E)

Example 5

Source: stock.xchng

Let's try a new probability experiment. This time, consider a bag of marbles, containing 10 red, 20 blue, and 15 green marbles. Suppose that two marbles are drawn without replacement. (The first marble is not put back in the bag before drawing the second.)

What is the probability that both marbles drawn are red?

[reveal answer]

Let's define a couple events:

E = first marble is red

F = second marble is red

We want P(E and F). Using the General Multiplication Rule, we see

P(E and F) = P(E) • P(F|E) = (10/45) • (9/44) ≈ 0.0455

Checking for Independence

If you recall, in Section 5.3, we defined what it meant for two events to be independent:

Two events E and F are independent if the occurrence of event E does not affect the probability of event F.

Looking at this in terms of conditional probability, if the occurrence of E doesn't affect the probability of F, then P(F|E) = P(F). This is a good way to test for independence. In fact, we can redefine independence using this concept.

Two events E and F are independent if P(F|E) = P(F).

Let's use this new definition in an example to determine if two events are independent.

Example 6

Let's again use the data from Example 3 and the survey given to 52 students in a Basic Algebra course at ECC, with the following responses to the statement "I enjoy math."

	Strongly Agree	Agree	Neutral	Disagree	Strongly Disagree	Total
Male	6	10	3	0	0	19
Female	8	14	7	4	0	33
Total	14	24	10	4	0	52

Suppose a student is selected at random from those surveyed and we define the events E and F as follows:

E = student selected is female

F = student enjoys math

Are events E and F independent?

[reveal answer]

To answer this, we'll need to see if P(F|E) = P(F).

P(F) = 38/52 ≈ 0.7308

P(F|E) = 22/33 ≈ 0.6667

Since P(F) ≠ P(F|E), events E and F are dependent.