Section 3.5: The Five-Number Summary and Boxplots

Objectives

By the end of this lesson, you will be able to...

compute the five-number summary
draw and interpret boxplots

For a quick overview of this section, watch this short video summary:

The Five-Number Summary

The five-number summary of a set of data consists of the smallest data value, Q₁, the median, Q₃, and the largest value of the data.

Example 1

To illustrate, let's again look at those exam scores from Example 4 in Section 3.4.

48	57	58	65	68	69	71	73	73
74	75	77	78	78	78	79	80	85
87	88	89	89	89	95	96	97	99

Find the five-number summary.

[ reveal answer ]

From Example 4 in Section 3.4, we already know that Q₁ = 71, median 78, and Q₃ = 89. We only need the maximum and minimum, so the five-number summary is:

minimum = 48
Q₁ = 71
median 78
Q₃ = 89
maximum = 99

Boxplots

Using the five-number summary and the fences, we can create a new graph called a boxplot.

Drawing a Boxplot

Step 1: Determine the five-number summary and the lower and upper fences.
Step 2: Draw a horizontal line and label it with an appropriate scale.
Step 3: Draw vertical lines at Q₁ , M, and Q₃. Enclose these vertical lines in a box.
Step 4: Draw a line from Q1 to the smallest data value that is within the lower fence. Similarly, draw a line from Q3 to the largest value that is within the upper fence.
Step 5: Any values outside the fences are outliers and are marked with an asterisk (*).

A typical boxplot will look something like this:

boxplot

Example 2

To illustrate, let's again look at those exam scores from Example 4 in Section 3.4.

48	57	58	65	68	69	71	73	73
74	75	77	78	78	78	79	80	85
87	88	89	89	89	95	96	97	99

Take a moment and try to sketch a boxplot of this data set, following the description above.

[ reveal answer ]

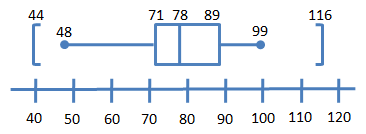
Using the five-number summary from Example 1 above and the outlier calculation from Example 5 in Section 3.4, we have the following information:

minimum = 48
Q₁ = 71
median 78
Q₃ = 89
maximum = 99
Lower fence = 44
Upper fence = 116

A boxplot would then look something like this:

example boxplot

Technology

Here's a quick overview of how to create box plots in StatCrunch.

Select Graphics > Box Plot.
Select the variable(s) you want to graph.
Check "Use fences to identify outliers".
Enter any modifications.
Choose a color scheme, if you wish, and click Compute.

Boxplots and Distribution Shape

The last thing we want to talk about in Chapter 3 is the relationship between the shape of a boxplot and the shape of the distribution.

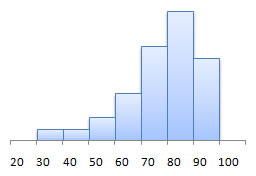
In Section 2.2, we talked about distribution shape, showing the following four standards:

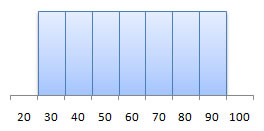uniform	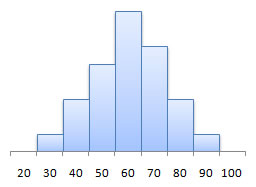symmetric (bell-shaped)
left-skewed	right-skewed

Let's now see how these are related to boxplots. Here's some information from your text:

Symmetric distributions

Distribution	Boxplot
Q₁ is equally far from the median as Q₃ is	The median line is in the center of the box
The minimum is equally far from the median as the maximum is	The left whisker is equal in length to the right whisker

symmetric

Skewed left distributions

Distribution	Boxplot
Q₁ is further from the median as Q₃ is	The median line is to the right of center in the box
The minimum is further from the median as the maximum is	The left whisker is longer than the right whisker

left-skewed

Skewed right distributions

Distribution	Boxplot
Q₁ is closer to the median than Q₃ is	The median line is to the left of center in the box
The minimum is closer to the median as the maximum is	The left whisker is shorter than the right whisker

right-skewed