home 1 2 3 4 5 6 7 8 9 10 11 12 13 Print

Section 3.4: Measures of Position

Objectives

By the end of this lesson, you will be able to...

  1. determine and interpret z-scores
  2. determine and interpret percentiles
  3. determine and interpret quartiles
  4. check a set of data for outliers

In Sections 3.1 and 3.2, we discussed ways to describe a "typical" individual in a population or sample. In this next section, we'll talk about ways to describe an individual in relation to the population.

For a quick overview of this section, watch this short video summary:

z-Scores

Example 1

It's fairly common for upper-level statistics courses to have both undergraduate and graduate students. Given the exam scores listed below, can you determine which score is better relative to its peers, the undergraduate score of 83 or the graduate score of 88?

undergraduate
student scores
65 89 84 75
52 78 92 80
76 72 83 79
graduate
student scores
82 90 95 72
78 88 92 89

Actually, to answer this question, we need more information. In particular, we need a new way to describe relative position.

The z-score represents the number of standard deviations a data value is from the mean.

Population z-Score Sample z-Score
z =  x - μ
σ
z ≈  x - x-bar
s

I can't over-emphasize the importance of the meaning behind the z-score. Make a note of this now - you'll be seeing this again later on in the semester - it's very important!

Example 1
(continued)

So let's continue with our previous example. The sample mean of the undergraduate scores is 77.1, with a standard deviation of 10.73. That gives a z-score for the undergraduate 83 of:

z =  83 - 77.1  ≈0.55
10.73

With a sample mean of 85.75 and a standard deviation of 7.78, the graduate has a z-score of:

z =  88 - 85.75  ≈0.29
7.76

Since the undergraduate is more than 1/2 of a standard deviation above the mean (z = 0.55), that's a better relative score.

Note: You may have noticed that I went to the hundredths place for these z-scores. That's standard practice.

Key: We use z-scores when we want to compare two individuals from different populations, relative to their respective populations.

Percentiles

If you've ever taken a standardized exam like the PSAT, SAT, or ACT, you've seen in the report something about your percentile.

The kth percentile, denoted Pk, of a set of data divides the lower k% of a data set from the upper (100-k)%.

Percentile ranks are used in a variety of fields:

Unfortunately, there's no universally accepted way to calculate percentiles. Most software packages and calculators use a method similar to the one below (from your text), but you should be aware of the possibility of others.

Determining the kth percentile, denoted Pk

  • Step 1: Arrange the data in ascending order.
  • Step 2: Compute an index i using the formula
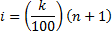
    percentile rank calculation
  • Step 3:
    1. If i is an integer, the kth percentile, denoted Pk, is the ith value.
    2. If i is not an integer, the kth percentile is the mean of the observations on either side of i.

Example 2

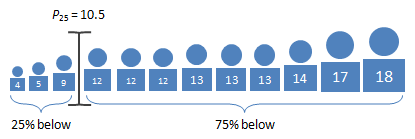
Let's go back to the Jackson cousins we saw in Example 2 in Section 3.1. Suppose this time we add all the cousins, from little Zander at age 4 to Mae, who at age 18 is entering her first year at college.

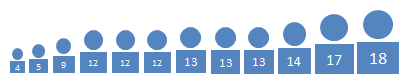
Jackson cousins in order

Use the strategy above to find the 25th percentile by age.

[ reveal answer ]

Technology

Here's a quick overview of the formulas for finding percentiles in StatCrunch.

  1. Select Stat > Summary Stat > Columns.
  2. Select the variable you want to summarize (e.g., "Heights")--leave everything else as is for now.
  3. Click "Next".
  4. Deselect any statistics that you do not want calculated
  5. Enter the percentile you wish to calculate in the "Percentile" box.
  6. Click "Calculate" and another window with these numbers calculated will pop up. 

Note: Some software like Microsoft Excel interpolates instead of taking a simple average when calculating percentiles, so the results may differ slightly.

Determining the Percentile of a Data Value

The last thing we need to do with percentiles is to figure out the percentile of a particular individual. For example, if your Composite ACT score is a 28, what percentile does that leave you?

As before, there is no universally accepted way to calculate percentiles, but the following (from your text) is very common.

Finding the Percentile that Corresponds to a Data Value

  • Step 1: Arrange the data in ascending order.
  • Step 2: Use the following formula to find the percentile of the value, x.
    percentile of x =   number of data values less than x *100
    n

Round this number to the nearest integer.

Example 3

Consider again the Jackson cousins we looked at in Example 2 above.

Jackson cousins in order

What is the percentile rank of James, the 14-year-old?

[ reveal answer ]

Using the formula above, we calculate i as:

percentile of James =   9 *100 = 75
12

So James is the 75th percentile.

Quartiles

As the name implies, quartiles divide the data into four equal parts. Therefore the first quartile, Q1, is the 25th percentile, the second quartile, Q2 is the 50th percentile (or the median), and the third quartile, Q3, is the 75th percentile.

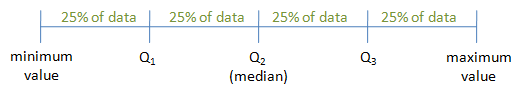
quartiles

Example 4

Let's consider one of the sets of hypothetical exam scores we looked at in Section 3.2.

48
 57 58 65 68 69 71 73 73
74 75 77 78 78 78 79 80 85
87 88 89 89 89 95 96 97 99

Find the quartiles.

[ reveal answer ]

Q1: 1st quartile 
So the 1st quartile is x7, or 71.

Q2: Since there are 27 observations, the median is x14, or 78.

Q3: 3rd quartile 
So the 3rd quartile is x21, or 89.

Technology

Here's a quick overview of the formulas for finding quartiles in StatCrunch.

  1. Select Stat > Summary Stat > Columns.
  2. Select the variable you want to summarize (e.g., "Heights")--leave everything else as is for now.
  3. Click "Next".
  4. Deselect any statistics that you do not want calculated
  5. Click "Calculate" and another window with these numbers calculated will pop up. 

Note: Some software like Microsoft Excel interpolates instead of taking a simple average when calculating percentiles, so the results may differ slightly.

Checking for Outliers

One good use of quartiles is they give us a sense of what values might be extreme. In Statistics, we call these values outliers. There are various ways to check for outliers. Most depend on the distribution and often can only characterize observations as possible outliers. A common technique used is the following:

Checking for Outliers by Using Quartiles

  • Step 1: Determine the first and third quartiles
  • Step 2: Compute the inter-quartile range: IQR = Q3 - Q1
  • Step 3: Determine the fences.
    1. Lower fence = Q1 - 1.5(IQR)
    2. Upper fence = Q3 + 1.5(IQR)
  • Step 4: If a value is less than the lower fence or greater than the upper fence it is considered an outlier.

Example 5

Let's look at those same exam scores we used in Example 4.

48
 57 58 65 68 69 71 73 73
74 75 77 78 78 78 79 80 85
87 88 89 89 89 95 96 97 99

Use the above method to determine if there are any outliers.

[ reveal answer ]

IQR = Q3 - Q1 = 89-71 = 18

Lower fence = Q1 - 1.5(IQR) = 71 - 1.5(18) = 44

Upper fence = Q3 + 1.5(IQR) = 89 + 1.5(18) = 116

Since no values lie outside the fences, there are no outliers.

 

<< previous section | next section >>

home 1 2 3 4 5 6 7 8 9 10 11 12 13 Print