Section 3.3: Measures of Central Tendency and Dispersion from Grouped Data

Objectives

By the end of this lesson, you will be able to...

approximate the mean and standard deviation of a variable from grouped data*
compute the weighted mean

* You will not be tested on this objective.

For a quick overview of this section, watch this short video summary:

Suppose you wanted to estimate the mean and standard deviation for an exam, but all the professor gave you was curve, maybe something like this one:

Exam 1 Scores
90+	8
80-89	13
70-79	6
60-69	3
50-59	1

Could you do it? How?

Approximating the Mean from Grouped Data

The technique we'll use (which you may have already thought of) is to treat each individual as the midpoint of its class. So instead of 13 scores from 80-89, we'll say that there are 13 85's. (This really works best with continuous data - we should probably use a midpoint of 84 for this example. Can you see why?)

From there, we should be able to approximate both the mean and standard deviation. We just have to remember to weight each observation by the number that are in that category.

Example 1

Using the Exam 1 data from above,

Scores	Freq	Midpoint
90+	8	95	8*95 = 760
80-89	13	85	13*85 = 1105
70-79	6	75	6*75 = 450
60-69	3	65	3*65 = 195
50-59	1	55	1*55 = 55
	31		2565

So the sample mean is then:

2565	≈82.7
31

(Notice again that I'm rounding the mean to one extra decimal place.)

Let's try the sample standard deviation:

Scores	Freq	Mdpt	x_i-	(x_i-)²
90+	8	95	12.3	151.29	8*151.29 = 1210.32
80-89	13	85	2.3	5.29	13*5.29 = 68.77
70-79	6	75	-7.7	59.29	6*59.29 = 355.74
60-69	3	65	-17.7	313.29	3*313.29 = 939.87
50-59	1	55	-27.7	767.29	1*767.29 = 767.29
	31				3341.99

The approximate sample standard deviation is then:

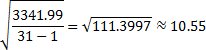
approximate sample standard deviation

Technology

To calculate the mean or standard deviation of variables from grouped data in StatCrunch, we assume that the data are already provided in "bins" within StatCrunch.

Be sure that the data are in "bins", with the bins formatted something like "0 to 4.9", "5 to 9.9" etc. in one column, with the counts in a second column.
Click on Stat > Summary Stats > Grouped/Binned data
Select the columns that the bins and counts are in.
Determine how you want midpoints to be defined. (Some texts uses "Consecutive lower limits, but there is also an argument for averaging the "Limits" instead.)
Select your statistics and click Compute.

Here's an example in YouTube by another instructor showing this process with a problem in MyStatLab: https://youtu.be/jBZMVS9w0PE

Weighted Mean

A weighted mean occurs when certain values carry more weight than others. The easiest example is your GPA. An "A" in Statistics counts more than an "C" in Tennis - not because it's more important or carries a higher meaning, but because the 4 credits for Statistics outweigh the 1 credit for Tennis. That's why your GPA will be closer to an "A" than a "C" - the Statistics course counts for more.

Here's how it works:

Each letter grade is assigned a weight. At most schools, this means an A=4, B=3, etc. Some schools do have other point systems, and there are many schools that have partial points with A-, B+, etc.

When calculating your GPA, the point value for each course is weighted by the number of credits. In the quick example above, your GPA for that semester wouldn't be a "B", because the Statistics course was worth 4 credits. The real GPA would be:

GPA =	weighted points	=	44 + 21	=	18	≈3.6
	total credits		4+1		5

Let's try one that's more interesting.

Example 2

Here's a typical course load for a 1st-year student at ECC, along with some typical grades.

Class	Credits	Grade
Statistics	4	B
Chemistry	5	A
Tennis	1	B
English	3	C
Speech	3	B

What is this student's semester GPA?

[ reveal answer ]

GPA =	43 + 54 + 13 + 32 + 3*3	=	50	≈ 3.125
	4 + 5 + 1 + 3 + 3		16

Technology

Calculating a weighted mean in StatCrunch

Click on Stat > Summary Stats > Grouped/Binned data
Select the columns that the values and weights are in.
Select the mean and click Compute.