Section 4.2: Least-Squares Regression
Objectives
By the end of this lesson, you will be able to...
- find the least-squares regression (LSR) line
- use the LSR line to make predictions
- interpret the slope and y-intercept of the LSR line
For a quick overview of this section, watch this short video summary:
Because we'll be talking about the linear relationship between two variables, we need to first do a quick review of lines.
The Slope and Y-intercept
If there's one thing we all remember about lines, it's the slope-intercept form of a line:
The slope-intercept form of a line is
y = mx + b
where m is the slope of the line and b is the y-intercept.
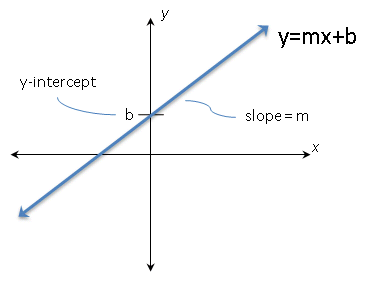
Knowing the form isn't enough, though. We also need to know what each part means. Let's start with the slope. Most of us remember the slope as "rise over run", but that only helps us graph lines. What we really need to know is what the slope represents in terms of the original two variables. Let's look at an example to see if we can get the idea.
Example 1
The equation T = 6x + 53 roughly approximates the tuition per credit at ECC since 2001. In this case, x represents the number of years since 2001 and T represents the tuition amount for that year.
The graph below illustrates the relationship.

In this example, we can see that both the 6 and the 53 have very specific meanings:
The 6 is the increase per year. In other words, for every additional year, the tuition increases $6.
The 53 represents the initial tuition, or the tuition per credit hour in 2001.
As we progress into the relationship between two variables, it's important to keep in mind these meanings behind the slope and y-intercept.
Finding the Equation for a Line
Another very important skill is finding the equation for a line. In particular, it's important for us to know how to find the equation when we're given two points.
A very useful equation to know is the point-slope form for a line.
The point-slope form of a line is
y - y1 = m(x - x1)
where m is the slope of the line and (x1, y1) is a point on the line.
Let's practice using this form to find an equation for the line.
Example 2
In Example 1 from section 4.1, we talked about the relationship between student heart rates (in beats per minute) before and after a brisk walk.
| before | after | before | after | before | after | ||
| 86 | 98 | 58 | 128 | 60 | 70 | ||
| 62 | 70 | 64 | 74 | 80 | 92 | ||
| 52 | 56 | 74 | 106 | 66 | 70 | ||
| 90 | 110 | 76 | 84 | 80 | 92 | ||
| 66 | 76 | 56 | 96 | 78 | 116 | ||
| 80 | 96 | 72 | 82 | 74 | 114 | ||
| 78 | 86 | 72 | 78 | 90 | 116 | ||
| 74 | 84 | 68 | 90 | 76 | 94 |
Let's highlight a pair of points on that plot and use those two points to find an equation for a line that might fit the scatter diagram.
Using the points (52, 56) and (90, 116), we get a slope of
| m = | 116-56 | = | 60 | ≈ 1.58 |
| 90-52 | 38 |
So an equation for the line would be:
y - y1 = m(x - x1)
y - 56 = 1.58(x - 52)
y - 56 = 1.58x - 82.16
y = 1.58x - 26.16
It's interesting to note the meanings behind the slope and y-intercept for this example. A slope of 1.58 means that for every additional beat per minute before the brisk walk, the heart rate after the walk was 1.58 faster.
The y-intercept, on the other hand, doesn't apply in this case. A y-intercept of -26.16 means that if you have 0 beats per minute before the walk, you'll have -26.16 beats per minute after the walk. ?!?!
This brings up a very important point - models have limitations. In this case, we say that the y-intercept is outside the scope of the model.
Now that we know how to find an equation that sort of fits the data, we need a strategy to find the best line. Let's work our way up to it.
Residuals
Unless the data line up perfectly, any line we use to model the relationship will have an error. We call this error the residual.
The residual is the difference between the observed and predicted values for y:
residual = observed y - predicted y
residual = ![]()
Notice here that we used the symbol ![]() (read
"y-hat") for the predicted. This is standard notation in statistics, using the "hat" symbol over
a variable to note that it is a predicted value.
(read
"y-hat") for the predicted. This is standard notation in statistics, using the "hat" symbol over
a variable to note that it is a predicted value.
Example 3
Let's again use the data from Example 1 from section 4.1. In Example 2 from earlier this section, we found the model:
![]() = 1.58x - 30.16
= 1.58x - 30.16

Let's use this model to predict the "after" heart rate for a particular students, the one whose "before" heart rate was 86 beats per minute.
The predicted heart rate, using the model above, is:
![]() = 1.58(86)
- 26.16 = 109.72
= 1.58(86)
- 26.16 = 109.72
Using that predicted heart rate, the residual is then:
residual = ![]() =
98 - 109.72 = -11.72
=
98 - 109.72 = -11.72
Here's that residual if we zoom in on that particular student:

Notice here that the residual is negative, since the predicted value was more than the actual observed "after" heart rate.
The Least-Squares Regression (LSR) line
So how do we determine which line is "best"? The most popular technique is to make the sum of the squares of the residuals as small as possible. (We use the squares for much the same reason we did when we defined the variance in Section 3.2.) The method is called the method of least squares, for obvious reasons!
The Equation for the Least-Squares Regression line
The equation of the least-squares is given by
![]()
where
![]() is the slope of
the least-squares regression line
is the slope of
the least-squares regression line
and
![]() is the y-intercept of the least squares regression line
is the y-intercept of the least squares regression line
Let's try an example.
Example 4
Let's again use the data from Example 1 in Section 4.1, but instead of just using two points to get a line, we'll use the method of least squares to find the Least-Squares Regression line.
| before | after | before | after | before | after | ||
| 86 | 98 | 58 | 128 | 60 | 70 | ||
| 62 | 70 | 64 | 74 | 80 | 92 | ||
| 52 | 56 | 74 | 106 | 66 | 70 | ||
| 90 | 110 | 76 | 84 | 80 | 92 | ||
| 66 | 76 | 56 | 96 | 78 | 116 | ||
| 80 | 96 | 72 | 82 | 74 | 114 | ||
| 78 | 86 | 72 | 78 | 90 | 116 | ||
| 74 | 84 | 68 | 90 | 76 | 94 |

Using computer software, we find the following values:
![]() ≈72.16667
≈72.16667
sx ≈10.21366
![]() = 90.75
= 90.75
sy ≈17.78922
r ≈ 0.48649
Note: We don't want to round these values here, since they'll be used in the calculation for the correlation coefficient - only round at the very last step.
Using the formulas for the LSR line, we have
![]() = 0.8473x +
29.60
= 0.8473x +
29.60
(A good general guideline is to use 4 digits for the slope and y-intercept, though there is no strict rule.)

One thought that may come to mind here is that this doesn't really seem to fit the data as well as the one we did by picking two points! Actually, it does do a much better job fitting ALL of the data as well as possible - the previous line we did ourselves did not address most of the points that were above the main cluster. In the next section, we'll talk more about how outliers like the (58, 128) point far above the rest can affect a model like this one.
Technology
Here's a quick overview of how to find the Least-Squares Regression line in StatCrunch.
The fourth line shows the equation of the regression line. Note that it will not have x and y shown, but rather the names that you've given for x and y. For example: Avg. Final Grade = 88.73273 - 2.8272727 Num. Absences |
| You can also go to the video page for links to see videos in either Quicktime or iPod format. |
