Section 4.1: Scatter Diagrams and Correlation

1. 4.1 Scatter Diagrams and Correlation
2. 4.2 Least-Squares Regression
3. 4.3 Diagnostics on the Least-Squares Regression Line
4. 4.4 Contingency Tables and Association

For a quick overview of this section, watch this short video summary:

In Chapter 3, we looked at numerically summarizing data from one variable (univariate data), but newspaper articles and studies frequently describe the relationship between two variables (bivariate data). It's this second class that we'll be focusing on in Chapter 4.

There are plenty of variables which seem to be related. The links below are articles from various news sources, all discussing relationships between two variables.

In each case, there's a response variable (GPA, newborn's health, cancer levels) whose value can be explained at least in part by a predictor variable (SAT score, proximity to highways, weight-loss pill consumption).

Our goal in this chapter will be to find ways to describe relationships like the one between a student's SAT score and his/her GPA, and to describe the strength of that relationship.

First, we need a new type of graph.

Scatter Diagrams

Scatter diagrams are the easiest way to graphically represent the relationship between two quantitative variables. They're just x-y plots, with the predictor variable as the x and the response variable as the y.

Example 1

Here's an excellent video showing a scatter diagram on steroids created by the BBC:

Technology

Here's a quick overview of the steps for creating scatter diagrams in StatCrunch.

Select Graph > Scatter Plot Select the X and Y variables. Enter a title and labels for both axes, then click Compute.

You can also go to the video page for links to see videos in either Quicktime or iPod format.

Types of Relationships

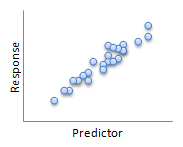
Not all relationships have to be linear, like the before/after heart rate data. The images below show some of the possibilities for the relationship (or lack thereof) between two variables.

The price of a manufactured item and the profit the company gains from it, for example, do not have a linear relationship. When prices are low, sales are high, but profit is still low since very little is made from each sale. As prices increase, profits increase, but at some point, sales will start to drop, until eventually too steep of a price will drive sales down so far as to not be profitable. This might be represented by the third, "Nonlinear" image.

 

Positive and Negative Association

The next thing we to do is somehow quantify the strength and direction of the relationship between two variables.

Here's how we'll describe the direction:

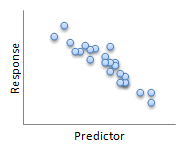
In general, we say two linearly related variables are positively associated if an increase in one is associated with an increase in the other (first "Linear" image). We say two linearly related variables are negatively associated if an increase in one is associated with a decrease in the other (second "Linear" image).

The images below show some examples of what scatter plots might look like for two positively associated variables.

And these are some examples of what scatter plots might look like for two negatively associated variables.

The Linear Correlation Coefficient

As we can see from these examples, knowing the directions isn't enough - we need to quantify the strength of the relationship as well. What we'll use to do that is a new statistic called the linear correlation coefficient. (In this class, we'll be dealing solely with linear relationships, so we usually just call it the correlation.)

I know that's quite a mouthful, but we'll be using technology to calculate it. Here's a quick summary of some of the properties of the linear correlation coefficient, as described in your text.

Next, I'd like you to visit two web sites that offer Java applets. These will help you interact with data to get a sense of the linear correlation coefficient.

Example 2

Example 3

Example 4

Technology

Here's a quick overview of the process for finding the linear correlation coefficient in StatCrunch.

Select Stat > Regression > Simple Linear Select the predictor variable for X & the response variable for Y Set any options, then click Compute Note that this output will include all of linear regression, including the linear correlation coefficient (r), finding the equation of the least squares regression line, computing the coefficient of determination, R2, and more.

Here's one for you to try.

Example 5

 

<< previous section | next section >>

1 2 3 4 5 6 7 8 9 10 11 12 13

This work is licensed under a Creative Commons License.