Section 1.3: Random Sampling

1. 1.1 Introduction to the Practice of Statistics
2. 1.2 Observational Studies versus Designed Experiments
3. 1.3 Random Sampling
4. 1.4 Bias in Sampling
5. 1.5 The Design of Experiments

For a quick overview of this section, watch this short video summary:

The next section we want to discuss is how to pick a "random" sample from a population. Even more-so - what does it mean to be "random"?

Why do we sample?

Let's suppose we want to know what ECC students think about parking on campus. It isn't possible to ask every single student, so instead we try to get a sample of students. One important characteristic that this sample must have is that it must be representative of the entire student body. (In other words, we can't have all Culinary Arts students, or all students that are fresh from high school.)

In this section and Section 1.4, we'll introduce several sampling strategies: simple random, stratified, systematic, and cluster.

Simple Random Sampling

The first type of sampling, called simple random sampling, is the simplest. Here's a definition:

A sample of size n from a population of size N is obtained through simple random sampling if every possible sample of size n has an equally likely chance of occurring.

OK, so maybe that didn't sound simple. Essentially, in order to qualify as a simple random sampling process, each sample must be equally likely. You've probably already used this method without knowing it.

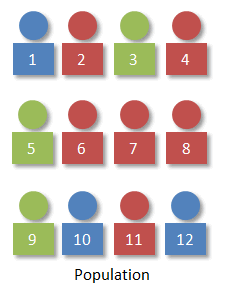
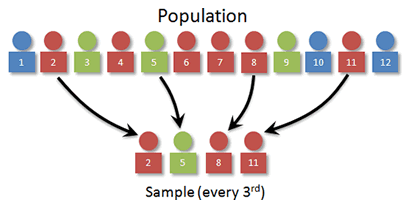
Let's suppose you want to select a sample of 4 people from a group of 12 (see image above). Here are some common ways to select a simple random sample:

• write everyone's name on a slip of paper and draw four from a hat
• write all possible samples of size four on slips of paper and draw one from a hat
• number each individual and use technology to randomly select four integers between 1 and 30

Practically, the first two lost their effectiveness with large groups, so we'll be focusing on the latter method.

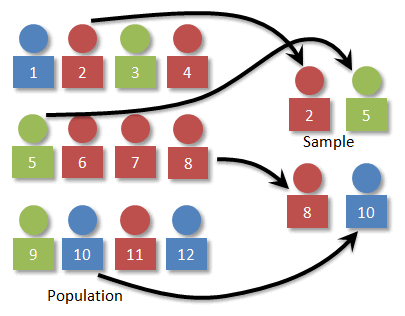
With our example of a sample size 4 from a population of 12, we might use technology to select four random integers between 1 and 12. Say we get 2, 5, 8, and 10. Our sample would then look this this:

For another take, watch this YouTube video by Steve Mays.

Random

The only thing left to do, then, is to generate a random number. But how do you do that? Just pick a number from your head?

For a good explanation, watch this video from Clive Rix, at the University of Leicester in England.

OK, then how do we actually generate a random number? The "Technology" box below shows how to generate what are called "pseudo random numbers", which is a reasonable enough technique for this course.

To get a true random number, you need something more sophisticated. One solution is random.org. For information about randomness and the difference between pseudo random numbers and true random numbers, you can visit their page on an Introduction to Randomness and Random Numbers.

For the purposes of this course, feel free to use the instructions below.

Technology

Here's a quick overview of how to generate random integers in StatCrunch.

Select Data > Simulate Data > Uniform Enter n for Rows and 1 for Columns Enter the lower and upper limits for a and b. Press Simulate You can manually round each value, or StatCrunch can do it for you. To round, follow these steps: Select Data > Compute expression Set Y to Uniform1. Select "round(Y)" in the expression dropbox (it's the very last expression). Press Set Expression and press Compute.

Stratified Sampling

Stratified sampling is different. With this technique, we separate the population using some characteristic, and then take a proportional random sample from each.

A stratified sample is obtained by separating the population into non-overlapping groups called strata and then obtaining a proportional simple random sample from each group. The individuals within each group should be similar in some way.

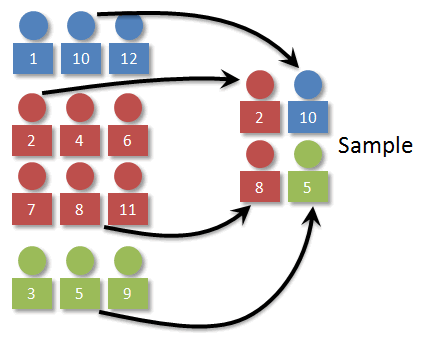
Visually, it might look something like the image below. With our population, we can easily separate the individuals by color.

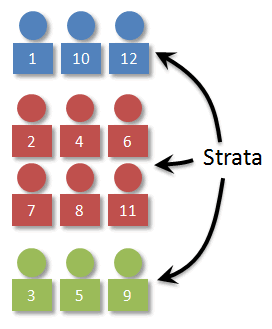
Once we have the strata determined, we need to decide how many individuals to select from each stratum. (Man, that's a weird word!) The key here is that the number selected should be proportional. In our case, 1/4 of the individuals in the population are blue, so 1/4 of the sample should be blue as well. Working things out, we can see that a stratified (by color) random sample of 4 should have 1 blue, 1 green, and 2 reds.

For another take, watch this YouTube video:

 

Example 1

Systematic Sampling

A systematic sample is obtained by selecting every kth individual from the population. The first individual selected corresponds to a random number between 1 and k.

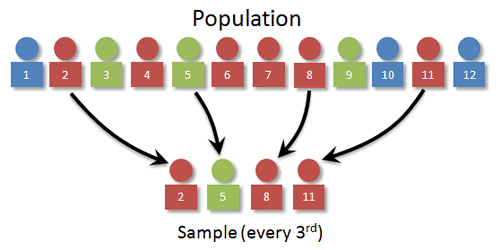
So to use systematic sampling, we need to first order our individuals, then select every kth. (More on how to select k in a bit.)

In our example, we want to use 3 for k? Can you see why? Think what would happen if we used 2 or 4.

For our starting point, we pick a random number between 1 and k. For our visual, let's suppose that we pick 2. The individuals sampled would then be 2, 5, 8, and 11.

In general we find k by taking N/n and rounding down to the nearest integer.

For another take, watch this YouTube video:

 

Example 2

Cluster Sampling

Cluster sampling is often confused with stratified sampling, because they both involve "groups". In reality, they're very different. In stratified sampling, we split the population up into groups (strata) based on some characteristic.

A cluster sample is obtained by selecting all individuals within a randomly selected collection or group of individuals.

In essence, we use cluster sampling when our population is already broken up into groups (clusters), and each cluster represents the population. That way, we just select a certain number of clusters.

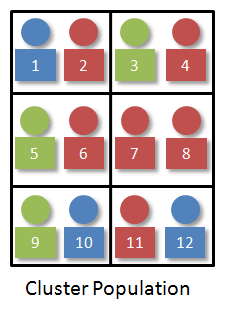
With our visual, let's suppose the 12 individuals are paired up just as they were sitting in the original population.

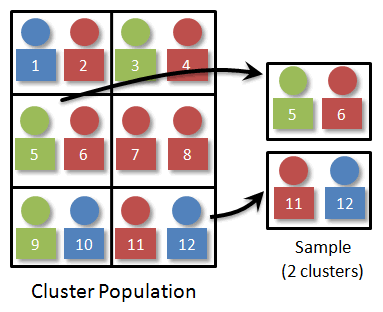
Since we want a random sample of size four, we just select two of the clusters. We would number the clusters 1-6 and use technology to randomly select two random numbers. It might look something like this:

For another take, watch this YouTube video:

 

Convenience Sampling

Other methods do exist for finding samples of populations. In fact, you've seen some already. Probably the most common is the so-called convenience sample. Convenience samples are just what they sound like - convenient. Unfortunately, they're rarely representative. Think of the radio call-in show, those people in the shopping malls trying to survey you about your purchasing habits, or even the voting on American Idol!

Here's a specific example. It's a poll on beliefnet.com, titled "What Evangelicals Want". All online polls use, by nature, convenience sampling. According to the article, "The poll was promoted on Beliefnet’s web site and through its newsletters." Only those evangelicals who visit this particular web site and actually answer the survey are included. Beware any poll result taken with convenience sampling.

Multistage Sampling

Often one technique isn't possible, so many professional polling agencies use a technique called multistage sampling. The strategy is relatively self-explanatory - two or more sampling techniques are used.

For example, consider the light-bulb example we looked at earlier with cluster sampling. Let's suppose that the bulbs come off the assembly line in boxes that each contain 20 packages of four bulbs each. One strategy would be to do the sample in two stages:

Stage 1: A quality control engineer removes every 200th box coming off the line. (The plant produces 5,000 boxes daily. (This is systematic sampling.)

Stage 2: From each box, the engineer then samples three packages to inspect. (This is an example of cluster sampling.)

The US Census also uses multistage sampling. For more information, you can check out this page from the US Census Bureau.

Summary

Here's a visual summary of the four main sampling strategies:

Simple Random:

Stratified:

Systematic:

Cluster:

<< previous section | next section >>

1 2 3 4 5 6 7 8 9 10 11 12 13

This work is licensed under a Creative Commons License.