Section 1.1: Introduction to the Practice of Statistics

1. 1.1 Introduction to the Practice of Statistics
2. 1.2 Observational Studies versus Designed Experiments
3. 1.3 Random Sampling
4. 1.4 Bias in Sampling
5. 1.5 The Design of Experiments

For a quick overview of this section, watch this short video summary:

The first thing we want to look at is exactly what "statistics" is. One reasonable definition might be:

Statistics is the science of collecting, organizing, summarizing, and analyzing information to draw conclusions or answer questions.

So what does that mean? Well, the reason we use data is that often the anecdotal information we have which might appear to be true actually is not.

Case in point: Recently the math department at ECC decided to do some investigation into the success of students in the College Algebra course. Many instructors had poor experiences with students who placed into the course with an ACT score of 23. Those faculty members felt that the cut-off score for placement into College Algebra should be increased to at least 24.

An interesting thing happened when data was collected from a year's worth of students - the students with a 23 on their ACT did just as well as students who placed their via ECC's own placement exam or those who took Intermediate Algebra first. Oops! This was a reminder to even those of us in the math department that there's a reason why the study of statistics was developed - we often have a skewed sense of reality when we only trust our experiences.

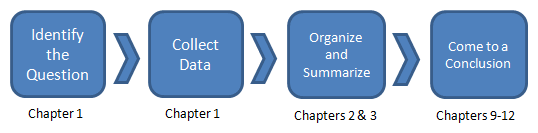
The Process of Statistics

So what exactly is the study of statistics? Well, it's really a process.

First, we must identify exactly what it is we're hoping to study. We must also determine what our population is.	Next, we select a representative sample using appropriate sampling techniques.	Once we have our data collected, we have to summarize it. We'll do this both numerically and visually with charts.	Finally, we need to analyze it and come to a conclusion.

The gaps in the middle - Chapters 4-8 - are a mix of sections. Chapter 4 really can stand on its own. It's all about analyzing the relationship between two variables. Chapters 5-8 involve probability and are intended as preparation for the meat of the course in Chapters 9-12.

Identifying the Question

A couple of key comments about identifying the question are needed here. The first thing we really need to consider is what our population is. The population is the group we're studying.

For example, if I'm interested in the studying habits of ECC students, then my population is all ECC students. Since asking every ECC student isn't possible, I would then take a sample, which is a subset of the population. The characteristics of the sample are key. If we select too few or the individuals selected don't represent the population, any conclusions we draw will be meaningless.

A statistic is a numerical summary of a sample. By contrast, a numerical summary of a population is called a parameter.

For example, if we know from ECC data that the average age of all ECC students is 29 (ECC College Facts), that value is a parameter. On the other hand, if we take a sample of 100 students and find that 63% support a new initiative at the college, that is a statistic - since it is only a measure of the sample of 100 students, not the entire student population.

When we simply describe or summarize data, we're using descriptive statistics. When we draw conclusions or extend our results to the population, we're using inferential statistics.

For example, the statistics of 63% from above would be a descriptive statistic, since it is simply a summary of our sample. If we, in turn, make a broad generalization and claim that 63% of all ECC students support the initiative, then that is inferential statistics.

Qualitative or Quantitative

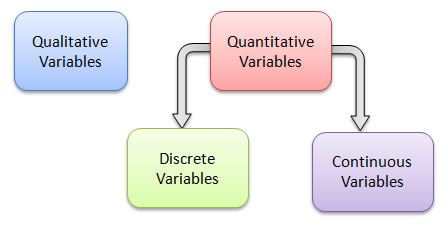
In general, we classify data into two groups: qualitative or quantitative.

Qualitative (or categorical) variables allow for classification of individuals based on some attribute or characteristic.

Quantitative variables provide numerical measures of individuals. Arithmetic operations such as addition and subtraction can be performed on the values of a quantitative variable and will provide meaningful results.

Basically, if a variable describes a quality of an individual - i.e. hair color, political party, etc - then it is qualitative. If a variable is numerical and those numbers have meaning, then it is quantitative. (Not all numbers have meaning numerically - think of an individuals Social Security number.)

Example 1

Discrete or Continuous

Quantitative variables can be further split into two groups.

A discrete variable is a quantitative variable that has either a finite number of possible values or a countable number of values. (Countable means that the values result from counting - 0, 1, 2, 3, ...)

A continuous variable is a quantitative variable that has an infinite number of possible values that are not countable.

Most variables are pretty clear, but some can be a bit tricky. An example of a tricky one is time. Say, for example, we're looking at how long we've been waiting for a bus. We count the minutes and seconds, but really those time units are only rounded. There are actually milliseconds, nanoseconds, etc - an infinite number of possibilities in the middle. So actually, any variable that is time is continuous.

Here's a graphical representation of the different ways to classify variables:

Example 2

Level of Measurement

Instead of categorizing variables into qualitative or quantitative, we can assign them various "levels" based on their characteristics.

Nominal: A nominal variable is one that simply categorizes or names the variables (i.e. "hair color"). This is the most general level of measurement.

Ordinal: An ordinal variable categorizes, but also has a specific order, like "course grade". This is a little more specific than a nominal variable.

Interval: An interval variable is quantitative (so the values have order as numbers), the differences between values have meaning, but a value of 0 doesn't mean the object has no value. The easiest example is "temperature" - clearly 60°F is more than 30°F, but 0°F doesn't mean it has no temperature and couldn't get colder.

Ratio: The final and most precise level of measurement is ratio. A ratio variable has all the properties of an interval variable, but the ratio of two values has meaning, and a value of zero means the absence of that quantity. A simple example might be "points earned on an exam". A score of 80 is twice the value of a score of 40, and a score of 0 clearly means the student earned no points on the exam. (Note that this is different than a grade of A vs. F, which would just be ordinal.)

Example 3

<< previous section | next section >>

1 2 3 4 5 6 7 8 9 10 11 12 13

This work is licensed under a Creative Commons License.