home 1 2 3 4 5 6 7 8 9 10 11 12 13 Print

Section 12.2: Tests for Independence and
the Homogeneity of Proportions

Objectives

By the end of this lesson, you will be able to...

  1. perform a test for independence
  2. perform a test for homogeneity of proportions

For a quick overview of this section, watch this short video summary:

In the previous section, we considered the relationship between a student's gender and whether he or she enjoys math. One question we might have as a result of this is whether we can determine whether there is a statistical test to determine if there is a relationship between the two variables.

Of course, we wouldn't be mentioning it if there wasn't! Before we discuss that test, we need a little background.

Determining Expected Counts

Let's assume that a student's gender and whether he or she enjoys math are independent. What frequencies would we expect in that case? Let's consider again the survey data from Example 2 in Section 4.4:

In that example, a survey was given to 82 students in a Basic Algebra course at ECC, with the following responses to the statement "I enjoy math."

  Strongly
Agree		 Agree Neutral Disagree Strongly
Disagree
Men 9 13 5 2 1
Women 12 18 11 6 5

We then created a relative frequency marginal distribution, which was calculated by taking the row/column totals and dividing by the sample size of 82.

  SA A N D SD Total
Men 9 13 5 2 1 30/82
≈ 0.37
Women 12 18 11 6 5 52/82
≈ 0.63
Total 21/82
≈ 0.26		 31/82
≈ 0.39		 16/82
≈ 0.20		 8/82
≈ 0.10		 6/82
= 0.07		 1

Let's focus on the first cell - "Men" and "Strongly Agree". From the table, we can see that 30/82 or about 37% of the students were men, and 21/82 or about 26% of the students strongly agreed with the statement "I enjoy math." If they really are independent, we can use the Multiplication Rule for independent events, where P(E and F) = P(E)•P(F).

So if they are independent, the probability that a student is is both male and strongly agrees would be:

P(male and strongly agrees) =  30 • 21  ≈ 0.094
82 82

We can then use this probability to determine how many we would expect in that cell, if the two variables are actually independent. We just multiply the total number of individuals by the probability of being both male and strongly agreeing:

Expected number of
students who are male
and strongly agree		  =  82• 30 • 21  =  30•21  ≈ 7.68
82 82 82

In general, we can find the expected values using this formula:

Expected Frequency  =  (row total)•(column total)  
table total

Example 1

Use the table provided and find the expected frequency for each outcome.

[ reveal answer ]

  SA A N D SD
Men 7.68 11.34 5.85 2.93 2.20
Women 13.32 19.66 10.15 5.07 3.80

Now that we have the expected frequencies for each outcome, we need a new hypothesis test to see if these expected counts are far enough from what we actually observed to say that the variables aren't independent.

 

The Test for Independence

The test we use to determine if there is an association between two qualitative variables is called the chi-square test for independence. In this test, the null hypothesis is always that the variables are not associated (independent), and the alternative is that they are associated (depedent).

The test works by comparing the observed counts with the expected counts if we assume the two variables are related. If those are far enough apart, we can say that we think there is a relationship. Here are the details:

The Test Statistic for the Test of Independence

If we let Oi represent the observed counts for the ith cell, and Ei represent the expected counts, then

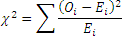
test statistic

approximately follows the chi-square distribution with (r-1)(c-1) degrees of freedom, where r is the number of rows and c is the number of columns, provided that:

  1. all expected frequencies are greater than or equal to 1, and
  2. no more than 20% of the expected frequencies are less than 5.

Note: If 1 or 2 fail, we can combine categories so they are satisifed.

Performing a Chi-Square Test for Independence

Step 1: State the null and alternative hypotheses.

H0: The row and column variables are independent.
H1: The row and column variables are dependent.

Note: Like the Goodness-of-Fit Test, this test is always right-tailed, since larger deviations from the expected values will result in larger Χ2 values.

Step 2: Decide on a level of significance, α.

Step 3: Compute the test statistic, test statistic.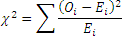

Step 4: Determine the P-value.

Step 5: Reject the null hypothesis if the P-value is less than the level of significance, α.

Step 6: State the conclusion.

Example 2

Use the data from earlier examples to determine if gender and whether a student enjoys math are related. Perform the test at the 5% level of significance.

From earlier, we have the observed counts:

  SA A N D SD
Men 9 13 5 2 1
Women 12 18 11 6 5

And from Example 1, we know the expected counts are:

  SA A N D SD
Men 7.68 11.34 5.85 2.93 2.20
Women 13.32 19.66 10.15 5.07 3.80

[ reveal answer ]

Notice that all expected counts are at least 1, but three are less than 5. Since 3 of 10 is 30%, we need to combine some categories. Our new observed and expected counts are then:

Observed SA A N D/SD
Men 9 13 5 3
Women 12 18 11 11
Expected SA A N D/SD
Men 7.68 11.34 5.85 5.12*
Women 13.32 19.66 10.15 8.88*

*Note: These values should be recalculated with the new observed counts, but they'll be close either way.

Step 1:
H0: gender and enjoying math are independent
H1: gender and enjoying math are dependent

Step 2: α = 0.05 (given)

Step 3:
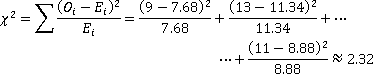
test statistic

Step 4: P-value = P(Χ2 > 2.32, df=3) ≈ 0.5085.

Step 5: Since the P-value is much larger than α, we do not reject the null hypothesis.

Step 6: No, there is clearly not enough evidence based on this sample to say that the variables are not independent. In other words, even though the expected counts are different from the observed counts, they're not different enough for us to say that the two couldn't be independent.

Chi-Square Test for Independence Using StatCrunch

With Data

  1. Select Stat > Tables > Contingency > With Summary
  2. Select theRow and Column variables
  3. (Optional) Select to Display Contributions to Chi-Square.
  4. Click Compute.

With Summary

  1. Select Stat > Tables > Contingency > With Summary
  2. Select the columns for the observed counts.
  3. Select the column for the Row labels.
  4. (Optional) Select to Display Contributions to Chi-Square.
  5. Click Compute.

The results should appear.

More information is available in the help file through StatCrunch.
videos You can also go to the video page for links to see videos in either Quicktime or iPod format.

Example 3

Repeat the previous example using technology.

[ reveal answer ]

Here are the results using StatCrunch:

StatCrunch calculations

We can see that the P-value is 0.5085, and so we have no evidence to say that there is an association between gender and whether or not a student enjoys math.

 

The Test for Homogeneity of Proportions

Suppose the Math Department at ECC would like to compare success rates in its College Algebra course based on how students placed into the class. There are currently three ways of placing into the course:

  1. earning a C or better in the Mth098 - Intermediate Algebra; or
  2. an appropriate placement test score; or
  3. a Math ACT of 23 or better.

In this case, the department might want to analyze the proportion who are successful in College Algebra (i.e. earning a C or better). They wonder if the proportions are all the same, or if one is different. One way to answer this would be to do proportion tests with all of the possible pairs, but that would entail three separate tests like those we studied in Section 11.3.

Another option is a new test - the chi-square test for homogeneity of proportions. In a chi-square test for homogeneity of proportions, we test the claim that different populations have the same proportion of individuals with a certain characteristic.

Interestingly, the procedures for performing a chi-square test for homogeneity of proportions is identical to that for the test of independence.

Example 4

In the Fall of 2005, the ECC math department asked the Institutional Research department to collect data from previous semesters to analyze. The table below shows the results for Fall 2004 and Spring 2005.

  Mth098 placement ACT 23+
successful 132 94 163
not successful 140 52 62

Is there evidence to indicate that the proportion of students in each group who are successful is different at the α = 0.01 level of significance?

[ reveal answer ]

Step 1:
H0: p1 = p2 = p3
H1: At least one of the proportions is different from the others.

Step 2: α = 0.01 (given)

Steps 3 & 4:

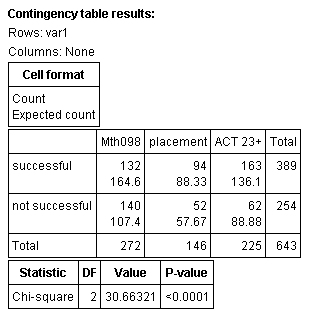
StatCrunch calculation

Step 5: Since the P-value < α, we should reject H0.

Step 6:Since the P-value is so small, we have very strong evidence suggesting that at least one of the proportions is different from the others.

 

<< previous section | next section >>

home 1 2 3 4 5 6 7 8 9 10 11 12 13 Print