Section 6.2: The Binomial Probability Distribution
Objectives
By the end of this lesson, you will be able to...
- determine whether a probability experiment is a binomial experiment
- compute probabilities of binomial experiments
- compute and interpret the mean and standard deviation of a binomial random variable
For a quick overview of this section, watch this short video summary:
Binomial Experiments
In the last section, we talked about some specific examples of random variables. In this next section, we deal with a particular type of random variable called a binomial random variable. Random variables of this type have several characteristics, but the key one is that the experiment that is being performed has only two possible outcomes - success or failure.
An example might be a free kick in soccer - either the player scores a goal or she doesn't. Another example would be a flipped coin - it's either heads or tails. A multiple choice test where you're totally guessing would be another example - each question is either right or wrong.
Let's be specific about the other key characteristics as well:
Criteria for a Binomial Probability Experiment
A binomial experiment is an experiment which satisfies these four conditions:
- A fixed number of trials
- Each trial is independent of the others
- There are only two outcomes
- The probability of each outcome remains constant from trial to trial.
In short: An experiment with a fixed number of independent trials, each of which can only have two possible outcomes.
(Since the trials are independent, the probability remains constant.)
If an experiment is a binomial experiment, then the random variable X = the number of successes is called a binomial random variable.
Let's look at a couple examples to check your understanding.
Example 1
Consider the experiment where three marbles are drawn without replacement from a bag containing 20 red and 40 blue marbles, and the number of red marbles drawn is recorded. Is this a binomial experiment?
No! The key here is the lack of independence - since the marbles are drawn without replacement, the marble drawn on the first will affect the probability of later marbles.
Example 2
A fair six-sided die is rolled ten times, and the number of 6's is recorded. Is this a binomial experiment?
Yes! There are fixed number of trials (ten rolls), each roll is independent of the others, there are only two outcomes (either it's a 6 or it isn't), and the probability of rolling a 6 is constant.
The Binomial Distribution
Once we determine that a random variable is a binomial random variable, the next question we might have would be how to calculate probabilities.
Let's consider the experiment where we take a multiple-choice quiz of four questions with four choices each, and the topic is something we have absolutely no knowledge. Say... theoretical astrophysics. If we let X = the number of correct answer, then X is a binomial random variable because
- there are a fixed number of questions (4)
- the questions are independent, since we're just guessing
- each question has two outcomes - we're right or wrong
- the probability of being correct is constant, since we're guessing: 1/4
So how can we find probabilities? Let's look at a tree diagram of the situation:

Finding the probability distribution of X involves a couple key concepts. First, notice that there are multiple ways to get 1, 2, or 3 questions correct. In fact, we can use combinations to figure out how many ways there are! Since P(X=3) is the same regardless of which 3 we get correct, we can just multiply the probability of one line by 4, since there are 4 ways to get 3 correct.
Not only that, since the questions are independent, we can just multiply the probability of getting each one correct or incorrect, so P(![]() ) = (3/4)3(1/4). Using that concept to find all the probabilities, we get the following distribution:
) = (3/4)3(1/4). Using that concept to find all the probabilities, we get the following distribution:
| x | P(x) |
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 |
We should notice a couple very important concepts. First, the number of possibilities for each value of X gets multiplied by the probability, and in general there are 4Cx ways to get X correct. Second, the exponents on the probabilities represent the number correct or incorrect, so don't stress out about the formula we're about to show. It's essentially:
P(X) = (ways to get X successes)•(prob of success)successes•(prob of failure)failures
The Binomial Probability Distribution Function
The probability of obtaining x successes in n independent trials of a binomial experiment, where the probability of success is p, is given by
![]()
Where x = 0, 1, 2, ... , n
Technology
Here's a quick overview of the formulas for finding binomial probabilities in StatCrunch.
|
Click on Stat > Calculators > Binomial Enter n, p, the appropriate equality/inequality, and x. The figure below shows P(X≥3) if n=4 and p=0.25.
|
Let's try some examples.
Example 3
Consider the example again with four multiple-choice questions of which you have no knowledge. What is the probability of getting exactly 3 questions correct?
For this example, n=4 and p=0.25. We want P(X=3).
We can either use the defining formula or software. The image below shows the calculation using StatCrunch.
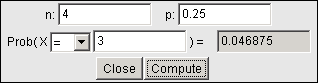
So it looks like P(X=3) ≈ 0.0469
(We usually round to 4 decimal places, if necessary.)
Example 4
A basketball player traditionally makes 85% of her free throws. Suppose she shoots 10 baskets and counts the number she makes. What is the probability that she makes less than 8 baskets?
If X = the number of made baskets, it's reasonable to say the distribution is binomial. (One could make an argument against independence, but we'll assume our player isn't affected by previous makes or misses.)
In this example, n=10 and p=0.85. We want P(X<8).
P(X<8) = P(X≤7) = P(X=0) + P(X=1) + ... + P(X=7)
Rather than computing each one independently, we'll use the binomial calculator in StatCrunch.

It looks like the probability of making less than 8 baskets is about 0.1798.
Example 5
Traditionally, about 70% of students in a particular Statistics course at ECC are successful. Suppose 20 students are selected at random from all previous students in this course. What is the probability that more than 15 of them will have been successful in the course?
Let's do a quick overview of the criteria for a binomial experiment to see if this fits.
- A fixed number of trials - The students are our trials.
- Each trial is independent of the others - Since they're randomly selected, we can assume they are independent of each other.
- There are only two outcomes - Each student either was successful or was not successful.
- The probability of each outcome remains constant from trial to trial. - Because the students were independent, we can assume this probability is constant.
If we let X = the number of students who were successful, it does look like X follows the binomial distribution. For this example, n=20 and p=0.70.
Let's use StatCrunch for this calculation:
So P(more than 15 were successful) ≈ 0.2375.
The Mean and Standard Deviation of a Binomial Random Variable
Let's consider the basketball player again. If she takes 100 free throws, how many would we expect her to make? (Remember that she historically makes 85% of her free throws.)
The answer, of course, is 85. That's 85% of 100.
We could do the same with any binomial random variable. In Example 5, we said that 70% of students are successful in the Statistics course. If we randomly sample 50 students, how many would we expect to have been successful?
Again, it's fairly straightforward - 70% of 50 is 35, so we'd expect 35.
Remember back in Section 6.1, we talked about the mean of a random variable as an expected value. We can do the same here and easily derive a formula for the mean of a binomial random variable, rather than using the definition. Just as we did in the previous two examples, we multiply the probability of success by the number of trials to get the expected number of successes.
Unfortunately, the standard deviation isn't as easy to understand, so we'll just give it here as a formula.
The Mean and Standard Deviation of a Binomial Random Variable
A binomial experiment with n independent trials and probability of success p has a mean and standard deviation given by the formulas
| and |
Let's try a quick example.
Example 6
Suppose you're taking another multiple choice test, this time covering particle physics. The test consists of 40 questions, each having 5 options. If you guess at all 40 questions, what are the mean and standard deviation of the number of correct answers?
If X = number of correct responses, this distribution follows the binomial distribution, with n = 40 and p = 1/5. Using the formulas, we have a mean of 8 and a standard deviation of about 2.53.
The Shape of a Binomial Probability Distribution
The best way to understand the effect of n and p on the shape of a binomial probability distribution is to look at some histograms, so let's look at some possibilities.
| n=10, p=0.2 | n=10, p=0.5 | n=10, p=0.8 |
 |
 |
 |
Based on these, it would appear that the distribution is symmetric only if p=0.5, but this isn't actually true. Watch what happens as the number of trials, n, increases:
| n=20, p=0.8 | n=50, p=0.8 |
 |
 |
Interestingly, the distribution shape becomes roughly symmetric when n is large, even if p isn't close to 0.5. This brings us to a key point:
As the number of trials in a binomial experiment increases, the probability distribution becomes bell-shaped. As a rule of thumb, if np(1-p)≥10, the distribution will be approximately bell-shaped.



