Section 7.3: Assessing Normality

Objectives

By the end of this lesson, you will be able to...

use normal probability plots to assess normality.

For a quick overview of this section, watch this short video summary:

Earlier in the course, in Section 2.2, we learned that we can characterize the distribution shape of a random variable using a histogram. One of those distribution shapes was bell-shaped (symmetric).

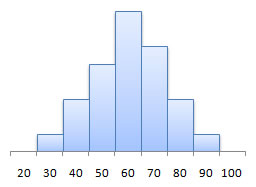
bell-shaped histogram

Later, in Section 7.1, we defined a normally distributed random variable to be one whose histogram follows the normal (bell-shaped) curve:

normal curve

So if we have the histogram, we can determine whether or not the random variable follows the normal distribution.

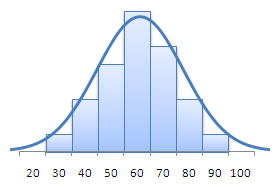
normal histogram

What happens, though, when the sample size is so small that we can't really see the distribution shape in the histogram? We need another method, which brings us to the topic for this section.

The Normal Probability Plot

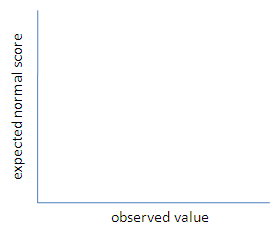
A normal probability plot is a graph that plots the observed data versus the normal score, which is what we would expect if the data actually followed the standard normal distribution.

In other words, if we have 15 observations, the 10th normal score would be the expected 10th value if the data followed the standard normal distribution.

normal probability plot

We know from earlier this section that

Z =	x - μ
	σ

If we solve this equation for X, we get X = μ + σZ, which is the equation for a line. This gets us to the key result:

If sample data are taken from a population that is normally distributed, a normal probability plot should be approximately linear.

Constructing a Normal Probability Plot Using Technology

Unfortunately, StatCrunch doesn't have a method of producing this plot, so we'll instead be doing a Q-Q plot, which is different but offers similar results.

Q-Q Plots in StatCrunch

Select Graphics > QQ Plot.
Select the column you want to plot, and click Compute.

You can also go to the video page for links to see videos in either Quicktime or iPod format.

Example 1

Suppose we wish to know whether the resting heart rates of a sample of Mth120 students are normally distributed.

heart rate
61	63	64	65	65
67	71	72	73	74
75	77	79	80	81
82	83	83	84	85
86	86	89	95	95

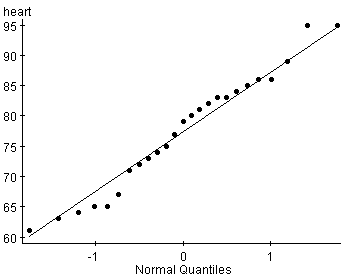
QQ plot

Based on this plot, it does appear as though the resting heart rates are approximately normally distributed. The plot is fairly linear, with just a couple points straying from the line.

Example 2

Suppose we wish to know whether the number of children that students in a particular Mth120 class have in their family is normally distributed.

number of children
3	4	3	1	5
3	2	4	2	5
9	2	3	2	7
3	1	2	6	2
4	3	1	2	2

QQ plot

This plot is clearly not linear, so the data do not come from a normally distributed population.