Section 2.1: Organizing Qualitative Data

Objectives

By the end of this section, you will be able to...

organize qualitative data in tables
organize quantitative data into tables
create cumulative frequency and relative frequency tables

For a quick overview of this section, watch this short video summary:

Frequency and Relative Frequency Tables

Let's suppose you give a survey concerning favorite color, and the data you collect looks something like the table below.

blue	red	blue	orange	blue	yellow	green	red	pink
blue	green	blue	purple	blue	blue	green	yellow	pink
blue	red	pink	green	blue	yellow	green	blue

Clearly, we need a better way to summarize the data. The most obvious thing to do would be to make a table with the list of favorite colors and the frequency for each.

favorite color	frequency
blue	10
red	3
orange	1
yellow	3
green	5
pink	3
purple	1

Officially, we call this a frequency distribution.

A frequency distribution lists each category of data and the number of occurrences for each category.

Sometimes, we really want to know the frequency of a particular category in reference to the total. We can do this just by finding the total, and dividing the frequency for each category by that total.

The relative frequency is the proportion (or percent) of observations within a category and is found using the formula

relative frequency =	frequency
	sum of all frequencies

A relative frequency distribution lists each category of data together with the relative frequency of each category.

favorite color	relative frequency
blue	10/26 ≈ 0.38
red	3/26 ≈ 0.12
orange	1/26 ≈ 0.04
yellow	3/26 ≈ 0.12
green	5/26 ≈ 0.19
pink	3/26 ≈ 0.12
purple	1/26 ≈ 0.04

Technology

Here's a quick overview of how to create frequency and relative frequency tables in StatCrunch.

Select Stat > Tables > Frequency.
Select the column(s) you want to summarize and click Next.
Add any modifications for an "Other" category and how to order the categories.
Click Calculate and another window with these numbers calculated will pop up.
You can then choose Options > Copy to copy the output for use elsewhere.

Organizing Discrete Data into Tables

If you recall from Section 1.2,

A discrete variable is a quantitative variable that has either a finite number of possible values or a countable number of values. (Countable means that the values result from counting - 0, 1, 2, 3, ...)

Since we can list all the possible values (that's essentially what countable means), one way to make a table is just to list the values along with their corresponding frequency.

Example 1

Here's some data I collected from a previous students Mth120 course. It refers to the number of children in their family (including themselves).

2	2	2	4	5	3	3	3	3
2	1	2	3	5	3	4	3	1
2	3	5	3	2	1	3	2

An easy way to compile the data would then be to make a frequency or relative frequency table as we did before.

children	frequency	relative frequency
1	3	3/26 ≈ 0.12
2	8	8/26 ≈ 0.31
3	10	10/26 ≈ 0.38
4	2	2/26 ≈ 0.08
5	3	3/26 ≈ 0.12

Sometimes, however, we have too many values to make a row for each one. In that case, we'll need to group several values together.

Example 2

A good example might be the scores on an exam, ranging from 1-100. Here are some data from a past Mth120 class.

62	87	67	58	95	94	91	69	52
76	82	85	91	60	77	72	83	79
63	88	79	88	70	75	87

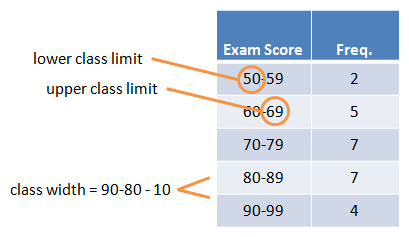
In this case, we'll have to set up intervals of numbers called classes. Each class has a lower class limit and an upper class limit, along with a class width. The class width is the difference between successive lower class limits.

To be consistent, the class width should be same for each class. One good option might look something like this:

frequency table

Organizing Continuous Data into Tables

Organizing continuous data is similar to organizing multi-valued discrete data. We have to form classes which don't overlap. I usually try to design a class width that's either logical (i.e. 10 points for grades above) or so that I have 5-8 classes when complete.

Example 3

For this example, let's consider the average commute for each of the 50 states. The data below show the average daily commute of a random sample of 15 states.

23.1	18.3	23.2	19.9	26.6
24.8	23.1	23.2	22.7	29.4
22.3	30.0	25.8	21.9	16.7
Source: US Census

Do you know why this is a continuous random variable and not discrete? (Hint: It's not because of the decimal.)

I think I know!

This is continuous because the variable we're measuring - time - is not finite. When, say, a marketing agent measures her commute time, she actually rounds to the nearest minute. If she reports 32 minutes, it's not exactly 32 minutes, it's 32 minute to the nearest minute. In reality, it might be 32.15323623245134... (you get the idea).

To make a frequency or relative frequency for continuous data, we use the same strategy we'd use for multi-valued discrete data.

average commute	frequency	relative frequency
16-17.9	1	1/15 ≈ 0.07
18-19.9	2	2/15 ≈ 0.13
20-21.9	1	1/15 ≈ 0.07
22-23.9	6	6/15 = 0.40
24-25.9	2	2/15 ≈ 0.13
26-27.9	1	1/15 ≈ 0.07
28-29.9	1	1/15 ≈ 0.07
30-31.9	1	1/15 ≈ 0.07

Once we have these tables, we'll need to learn how to create some charts to display the information, which is what the next few page are about.

Technology

Here's a quick overview of how to create frequency and relative frequency tables for quantitative data in StatCrunch.

Discrete Data

Select Stat > Tables > Frequency.
Select the column(s) you want to summarize and click Next.
Add any modifications for an "Other" category and how to order the categories, and click Calculate.

Continuous or Multi-valued Discrete Data:

Select Data > Bin Column.
Select the column containing the data, select "Use fixed width bins", and set the lowest class limit (Start bins at:) and class (bin) width.
Click Calculate.
Select Stat > Tables > Frequency.
Select the newly created bin column and click Calculate.*

* Note that these classes seem to overlap, but that the class "0-k" does not include Mk.

Creating a relative frequency table from a frequency table

If you are given a frequency table and need to create a relative frequency table, use the following steps, assuming that "Frequency" is the label of the column containing the frequencies - edit as needed.

Click on Data > Compute > Expression.
Enter the text "Frequency/sum(Frequency)" in the Expression box.
If desired, enter a column label.
Click Compute.

Cumulative Tables

Cumulative tables are just what they imply - they show the sum of values up to and including that particular category. As with regular tables, we can have both cumulative frequency and relative frequency.

Example 4

To illustrate the idea, let's look at the average commute data from the last section.

average commute	frequency	cumulative frequency
16-17.9	1	1
18-19.9	2	3
20-21.9	1	4
22-23.9	6	10
24-25.9	2	12
26-27.9	1	13
28-29.9	1	14
30-31.9	1	15

average commute	relative frequency	cumulative relative frequency
16-17.9	1/15 ≈ 0.07	1/15 ≈ 0.07
18-19.9	2/15 ≈ 0.13	3/15 ≈ 0.20
20-21.9	1/15 ≈ 0.07	4/15 ≈ 0.27
22-23.9	6/15 = 0.40	10/15 ≈ 0.67
24-25.9	2/15 ≈ 0.13	12/15 = 0.80
26-27.9	1/15 ≈ 0.07	13/15 ≈ 0.87
28-29.9	1/15 ≈ 0.07	14/15 ≈ 0.93
30-31.9	1/15 ≈ 0.07	15/15 = 1.00

Technology

Select Stat > Tables > Frequency.
Select the column(s) you want to summarize.
Select Cumulative frequency or Cumulative relative frequency as the Statistic(s).
Click Compute.

Creating cumulative tables from a frequency table.

Unfortunately, there is no easy way to create cumulative tables in StatCrunch. You actually need to write a custom function to do this.

Go to Data > Compute > Expression.
Enter cumsum([column name]) (Where [column name] is the column where the frequencies or relative frequencies are stored.)
If desired, enter a Column label.
Click Compute.