Section 13.1: Comparing Three or More Means (One-Way ANOVA)

Objectives

By the end of this lesson, you will be able to...

verify the requirements to perform a one-way ANOVA
test a hypothesis regarding three or more means using one-way ANOVA

For a quick overview of this section, watch this short video summary:

What is One-Way ANOVA?

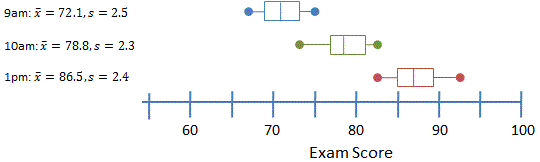
Suppose you're an instructor teaching three sections of the same course. You suspect that the three sections are not equivalent, but you can't be sure. Since the students won't always earn the same score on every exam, we can treat an individual exam given to all the students in each section as a "sample" from each section.

Suppose the results from the first turn out as follows:

We can clearly see that these appear to be from very different populations - the means are very different, and there's very little variation within each group. With that description, we can be pretty sure they're different.

What about a different situation?

In this case, we can see that the means do appear to be different, but not by much. And within each sample, there is a lot of variation, so the difference in the means could just be due to the wide variation within each group.

The point here is that we can't just consider the differences in the means - whether those differences are significant or not depends on the standard deviations (and sample sizes, of course).

This is the basic idea behind One-Way ANOVA. It's one-way, because we're focusing on a single characteristic (time of class period, in our example above). And the ANOVA stands for analysis of variance. While it may seem odd that the title refers to variance when we're actually comparing means, it's actually because of a significant assumption - to perform the statistical analysis.

To perform the test, we focus on the between-sample variation (between the means) and the within-sample variation (i.e. the standard deviation). If the former is large in comparison to the latter, we can say that one of the means must be different. The test statistic that we use is another F-statistic, and it's the ratio of these two variations:

In order to analyze this statistic, though, there are several requirements that need to be met.

Verifying the Requirements

In order to perform one-way ANOVA, the following requirements must be met:

Requirements to Perform a One- Way ANOVA Test

There must be k simple random samples, one from each of k populations or a randomized experiment with k treatments.
The k samples must be independent of each other; that is, the subjects in one group cannot be related in any way to subjects in a second group.
The populations must be normally distributed.
The populations must have the same variance; that is, each treatment group has population variance σ².

Luckily, the procedure is robust, so slight variations from these criteria are OK. In particular, a good rule of thumb is that as long as the largest variance is no more than double the smallest, we can assume point #4 above has been satisfied. If not, there are other tests that can be performed, but they're beyond the scope of this course.

Example 1

Problem: Referring back to the example above, does it appear that the conditions are met to perform one-way ANOVA?

Solution: To answer this, let's consider the box plots we were provided:

Exam 1 results

Granted, the information is a little imprecise here, but we do have 3 samples that are independent (3 different sections). Based on the boxplots, the scores do appear to be normally distributed, though without a histogram that's difficult to tell precisely. And the largest standard deviation of 10.1 is not more than double the smallest of 8.7.

So yes, it does appear that the conditions have been met and one-way ANOVA could be performed.

Performing a Hypothesis Test Regarding Three or More Means Using One-Way ANOVA

Step 1: State the null and alternative hypotheses.

H₀: μ₁ = μ₂= μ₃ = ...
H₁: At least one of the means is different

Step 2: Decide on a level of significance, α.

Step 3: Compute the test statistic, (using StatCrunch).

Step 4: Determine the P-value.

Step 5: Reject the null hypothesis if the P-value is less than the level of significance, α.

Step 6: State the conclusion.

Hypothesis Testing Regarding Three or More Means Using One-Way ANOVA with StatCrunch

Data in Single Column with Grouping Variable

Go to Stat > ANOVA > One Way.
Select the columns you wish to compare.
Click Compute.

Data in Multiple Columns

Go to Stat > ANOVA > One Way.
Select "Compare values in a single column" and then choose the column that contains the values of the variables and the column that indicates the factor.
Click Compute.

The results should appear.

Example 2

Problem: Referring back to the example above, use the data provided in StatCrunch to answer the question.

Is there enough evidence at the 5% level of significance to support the claim that one of the classes is performing differently from the others?

Solution:

Assuming again the conditions have been met, we have the following results:

Step 1:

H₀: μ₁ = μ₂= μ₃ = ...
H₁: At least one of the means is different

Step 2: α = 0.05 (given)

Step 3: (we'll use StatCrunch)

Step 4: Using StatCrunch:

StatCrunch results

Step 5: Since the P-value > α, we do not reject the null hypothesis.

Step 6: There is not enough evidence at the 5% level of significance to support the claim that the mean score from one of these sections is different from the others.